

 Đã Đây là ý kiến của mk mk ko chắc đg nha!
Đã Đây là ý kiến của mk mk ko chắc đg nha!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


 Đã Đây là ý kiến của mk mk ko chắc đg nha!
Đã Đây là ý kiến của mk mk ko chắc đg nha!

a) ta có: tam giác ABC cân tại A
=> góc ABC = góc ACB ( tính chất tam giác cân)
mà góc ABC = góc HBD; góc ACB = góc KCE ( đối đỉnh)
=> góc HBD = góc KCE (= góc ABC = góc ACB)
Xét tam giác DHB vuông tại H và tam giác EKC vuông tại K
có: DB = EC (gt)
góc HBD = góc KCE (cmt)
\(\Rightarrow\Delta DHB=\Delta EKC\left(ch-gn\right)\)
=> HB = KC ( 2 cạnh tương ứng)
b) ta có: góc ABC + góc ABH = 180 độ ( kề bù)
góc ACB + góc ACK = 180 độ ( kề bù)
=> góc ABC + góc ABH = góc ACB + góc ACK ( = 180 độ)
=> góc ABH = góc ACK ( góc ABC = góc ACB)
Xét tam giác ABH và tam giác ACK
có: AB = AC (gt)
góc ABH = góc ACK
BH = CK (phần a)
\(\Rightarrow\Delta ABH=\Delta ACK\left(c-g-c\right)\)
\(\Rightarrow\widehat{AHB}=\widehat{AKC}\) ( 2 góc tương ứng)
c) ( Nối H với E)
ta có: \(DH\perp BC⋮H\)
\(EK\perp BC⋮K\)
\(\Rightarrow DH//EK\) ( định lí từ vuông góc đến //)
=> góc DHE = góc KEH ( so le trong)
ta có: tam giác DHB = tam giác EKC ( phần a)
=> DH = EK ( 2 cạnh tương ứng)
Xét tam giác DHE và tam giác KEH
có: DH = KE ( cmt)
góc DHE = góc KEH (cmt)
HE là cạnh chung
\(\Rightarrow\Delta DHE=\Delta KEH\left(c-g-c\right)\)
\(\Rightarrow\widehat{DEH}=\widehat{KHE}\) ( 2 góc tương ứng)
mà góc DEH và góc KHE nằm ở vị trí so le trong
=> HK // DE ( định lí //)
d) ta có: \(\Delta ABH=\Delta ACK\) ( phần b)
=> AH = AK ( 2 cạnh tương ứng)
góc BAH = góc CAK ( 2 góc tương ứng)
=> góc BAH + góc BAC = góc CAK + góc BAC
=> góc HAE = góc KAD
ta có: AB = AC; BD = CE
=> AB + BD = AC + CE
=> AD = AE
Xét tam giác AHE và tam giác AKD
có: AE = AD (cmt)
góc HAE = góc KAD (cmt)
AH = AK ( cmt)
\(\Rightarrow\Delta AHE=\Delta AKD\left(c-g-c\right)\)

mấy câu a,b,c,d chắc bạn biết làm hết rồi nên mình giải câu e nha
cmd tam gi1c ahi=aki(c.c.c)suy ra góc hai=kai
cmđ dai=eai
gọi giao điểm của ai va bc la kcòn với de là n
cmd tam giac bak=cak suy ra gó akb=akc =90 độ
tương tự cmd and =90 độ
vậy ai vuông góc với de
mình bận nên ghi hơi tat nên chổ nào bạn ko hiểu ở bài này có the hoi mình ,nếu bnko hieu caub,c,d có thể hỏi mình
mấy câu a,b,c,d chắc bạn biết làm hết rồi nên mình giải câu e nha
cmd tam gi1c ahi=aki(c.c.c)suy ra góc hai=kai
cmđ dai=eai
gọi giao điểm của ai va bc la kcòn với de là n
cmd tam giac bak=cak suy ra gó akb=akc =90 độ
tương tự cmd and =90 độ
vậy ai vuông góc với de
chúc bn hok tốt @_@

a,Ta có: góc HBD=góc ABC
góc KCE = góc ACB
Mà góc ABC = góc ACB ( tam giác ABC cân)
Xét tam giác BDH và tam giác CEK:
Góc DHB = góc EKC
BD=CE (GT)
Góc HBD = góc KCE (cmt)
=> tam giác BDH = tam giác CEK ( cạnh huyền - góc nhọn )
b, Ta có: AB=AC;BD=CE
=> AB+BD=AC+CE
<=>AD=AE
Xét tam giác AHD và tam giác AKE:
HD=KE(tam giác BDH = tam giác CEK)
Góc HDB=góc KEC(tam giác BDH = tam giác CEK)
AD=AE(cmt)
=> tam giác AHD = tam giác AKE
=>AH=AK và góc HAD = góc KAE
Xét tam giác AHB và tam giác AKC
AH=AK(cmt)
góc HAB = góc KAC(cmt)
AB=AC( tam giác ABC cân)
=> tam giác AHB = tam giác AKC
=> Góc AHB = góc AKC

A B C H K I D E
a) Tao có :) \(\Delta ABC\)cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
T lại có :) \(\widehat{ABC}=\widehat{HBD}\left(đđ\right)\)
\(\widehat{ACB}=\widehat{KCE}\left(đđ\right)\)
\(\Rightarrow\widehat{HBD}=\widehat{KCE}\)
Xét \(\Delta HBD\)và \(\Delta KCE\)t có :)
\(\widehat{HBD}=\widehat{KCE}\)
\(BD=CE\)
\(\widehat{DHB}=\widehat{EKC}\left(=90^o\right)\)
\(\Rightarrow\Delta HBD=\Delta KCE\left(ch-gn\right)\)
\(\Rightarrow HB=KC\left(đpcm\right)\)
b) T có :) \(\widehat{ABH}+\widehat{ABC}=180^o\)( kề bù )
\(\widehat{ACK}+\widehat{ACB}=180^o\)( kề bù )
Mà :) \(\widehat{ABC}=\widehat{ACB}\)
\(\Rightarrow\widehat{ABH}=\widehat{ACK}\)
Xét \(\Delta AHB\)và \(\Delta AKC\)có :)
\(HB=CK\)
\(\widehat{ABH}=\widehat{ACK}\)
\(AB=AC\)
\(\Rightarrow\Delta AHB=\Delta AKC\left(c-g-c\right)\)
\(\Rightarrow\widehat{AHB}=\widehat{AKC}\left(đpcm\right)\)
c) Do \(\Delta ABC\)cân tại A \(\Rightarrow\widehat{ABC}=\frac{180^o-\widehat{BAC}}{2}\left(1\right)\)
Mà :) \(AB=AC\)
\(BD=CE\)
\(\Rightarrow AB+BD=AC+CE\)
\(\Rightarrow AD=AE\)
\(\Rightarrow\Delta ADE\)cân tại A \(\Rightarrow\widehat{ADE}=\frac{180^o-\widehat{BAC}}{2}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{ABC}=\widehat{ADE}\)
Mà hai góc trên đồng vị :)
\(\Rightarrow HK//DE\left(đpcm\right)\)
d) Theo câu b t có \(\Delta AHB=\Delta AKC\)
\(\Rightarrow\hept{\begin{cases}AH=AK\\\widehat{HAB}=\widehat{KAC}\end{cases}}\)
\(\Rightarrow\widehat{HAB}+\widehat{BAC}=\widehat{KAC}+\widehat{BAC}\)
\(\Leftrightarrow\widehat{HAC}=\widehat{KAB}\)
Xét \(\Delta AHE\)và \(\Delta AKD\)có :)
\(\widehat{HAC}=\widehat{KAB}\)
\(AH=AK\)
\(AE=AD\)
\(\Rightarrow\Delta AHE=\Delta AKD\left(c-g-c\right)\left(đpcm\right)\)
e) \(\Rightarrow\widehat{AHE}=\widehat{AKD}\)
\(\Leftrightarrow\widehat{AHK}+\widehat{KHE}=\widehat{AKH}+\widehat{HKD}\)
Mà :) \(\widehat{AHK}=\widehat{AKH}\)( câu b )
\(\Rightarrow\widehat{KHE}=\widehat{HKD}\Rightarrow\Delta HIK\)cân tại I
\(\Rightarrow HI=IK\)
Xét \(\Delta AHI\)và \(\Delta AKI\)có :)
\(HI=IK\)
\(AH=AK\)
Chung AI
\(\Rightarrow\Delta AHI=\Delta AKI\left(c-c-c\right)\)
\(\Rightarrow\widehat{HAI}=\widehat{KAI}\)
\(\Leftrightarrow\widehat{HAB}+\widehat{BAI}=\widehat{CAI}+\widehat{KAC}\)
Lại có :) \(\widehat{HAB}=\widehat{KAC}\)
\(\Rightarrow\widehat{BAI}=\widehat{CAI}\)
\(\Rightarrow\)AI là tia phân giác \(\widehat{BAC}\)hay \(\widehat{DAE}\)
Mà \(\Delta DAE\)cân tại A
\(\Rightarrow AI\perp DE\)( do đường phân giác của đỉnh tam giác cân cũng chính là đường cao của tam giác cân đó )
Vậy .... :)
Hình vẽ : 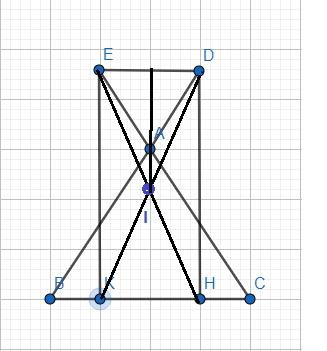
a) Dễ nhận thấy DE = KH = 1/2 BC
Do đó KH = 1/2BC suy ra KB + CH = 1/2BC=KH
Vậy KB + CH = KH
Do vậy 2KB + CH = KH + KB (1)
KB + 2CH = KH + KB (2)
Từ đó suy ra CH = KB
Mà HB = KH + KB (3)
CK = KH + HC (4)
Mà KB = HC nên KH + KB = KH + HC hay HB = CK
b) Chứng minh \(\Delta AHB=\Delta AKC\)
Ta có: \(\Delta AHB=\Delta AKC\left(c.g.c\right)\)
Suy ra \(\widehat{AHB}=\widehat{AKC}\)
c) Theo hình vẽ ta có BD = CE và BD là tia đối của BA, nên BD thẳng hàng với BA
CE là tia đối của CA nên CE thẳng hàng với CA
Do đó CE = BD . DO đó EK = DH.
Theo đề bài DH và EK cùng vuông góc BC (5) mà DH = EK do đó \(\widehat{D}=90^o;\widehat{E}=90^o\)(6)
Từ (5) và (6) suy ra HK song song DE
Sau đó tự làm tiếp

bạn vào đây nha
Câu hỏi của Phạm Mai Trang - Toán lớp 7 - Học toán với OnlineMath

1) đề có phải là: Cho tam giác ABC cân tại A, góc A nhỏ hơn 90 độ. Vẽ BD vuông AC và CE vuông AB. H là giao điểm của BD và CE.
a) Chứng minh Tam giác ABD = Tam giác ACE
b) Chứng minh tam giác AED cân
c, AH là đường trung trực của ED.
D) Trên tia đối DB lấy K sao cho DK = DB. Chứng minh góc ECB = Góc DKC
A B C D E H K
a) Xét tam giác ABD và tam giác ACE có:
\(\widehat{ACE}=\widehat{ABD}\left(cùngphuvoi\widehat{BAC}\right)\Rightarrow\Delta ABD=\Delta ACE\left(g.c.g\right)\hept{\begin{cases}AC=AB\left(\Delta ABCcântạiA\right)\\\widehat{BAC}chung\\\widehat{AEC}=\widehat{ADB}=90^o\end{cases}}\)
b) AE=AD(vì tam giác ABD=tam giác ACE
=> tam giác AED cân tại A
c) Xem lại đề
d) Xét tam giác BCK có:
\(\hept{\begin{cases}BK\perp DC\\BD=DK\end{cases}}\)
=> CD là đường trung trực của BK
=> BC=CK
=> tam giác BCK cân tại C
=>\(\widehat{CBK}=\widehat{CKB}\)
Mà \(\widehat{ECB}=\widehat{CBK}\)(vì góc ABC=góc ACB; góc ABD= góc ACE)
=> góc ECB= góc CKB
3) Đề là:
Cho góc xOy, vẽ tia phân giác Ot của góc xOy. Trên tia Ot lấy điểm M bất kì, trên tia Ox và Oy lần lượt lấy các điểm A và B sao cho OA = OB gọi H là giao điểm của AB và Ot . CHỨNG MINH:
a/ MA = MB
b/ OM là đường trung trực của AB
c/ Cho biết AB = 6cm; OA= 5cm. Tính OH ? (bn viết khó hiểu qá nên mk xem lại trong vở)
Tự vẽ hình!
a/ Xét tam giác OAM và tam giác OBM, có:
Cạnh OM là cạnh chung
OA = OB (gt)
góc AOM = góc BOM ( vì Ot là tia phân giác của góc xOy)
=> Tam giác OAM = tam giác OBM (c.g.c)
=> MA = MB ( 2 cạnh tương ứng)
b/ Ta có: MA = MB (cmt)
=> Tam giác AMB là tam giác cân
=> Góc MAH = góc MBH
Xét tam giác AMH và tam giác BMH, có:
góc MAH = góc MBH ( cmt)
MA = MB ( cmt)
góc AMH = góc BMH ( vì tam giác OAM = tam giác OBM)
=> tam giác AMH và tam giác BMH ( g.c.g)
=> AH = HB ( 2 cạnh tương ứng)
=> H là trung điểm của AB (1)
Vì tam giác AMH = tam giác BMH (cmt)
=>góc MHA = góc MHB ( 2 góc tương ứng)
mà góc MHA + góc MHB = 180 độ ( 2 góc kề bù)
=> góc MHA = góc MHB= 180 độ : 2 = 90 độ
=> MH vuông góc với AB (2)
Từ (1) và (2)
=> MH là đường trung trực của AB
=> OM là đường trung trực của AB ( vì H thuộc OM )
c/ Vì H là trung điểm của AB (cmt)
=> AH =HB = AB : 2 = 6 :2 = 3 (cm)
Xét tam giác OAH vuông tại H có: OA2 = OH2 + AH2 ( định lí Py-ta-go)
=> 52 = OH2 + 32
=> 25 = OH2 + 9
=> OH2 = 25 - 9
=> OH2 = 16
\(\Rightarrow OH=\sqrt{16}\)
\(\Rightarrow OH=4cm\)

Hình tự vẽ nha
a) Vì tam giác ABC cân tại A
=> ABC = ACB (1)
Ta có ABC + ABD = ACB + ACE ( cùng = 1800 ) (2)
Từ (1) và (2) => ABD = ACE
Xét tam giác ABD và tam giác ACE có :
AB = AC ( gt )
ABD = ACE ( cmt )
BD = CE ( gt )
=> tam giác ABD = tam giác ACE ( c-g-c )
=> D = E
Xét tam giác BHD và tam giác CKE có :
DHB = EKC ( = 900 )
BD = CE ( gt )
D = E ( cmt )
=> tam giác BHD = tam giác CKE ( ch - gn )
=> đpcm
b) Vì tam giác ABD = tam giác ACE ( chứng minh câu a )
=> HAB = KAC ( 2 góc tương ứng )
Xét tam giác AHB và tam giác AKC có :
HAB = KAC ( cmt )
AHB = AKC ( = 900 )
AB = AC ( gt )
=> tam giác AHB = tam giác AKC ( ch - gn )
=> đpcm
c) Nối H với K
Xét tam giác ADE cân tại A ( vì AD = AE )
=> \(\widehat{D}=\frac{180^0-\widehat{DAE}}{2}\left(1\right)\)
Xét tam giác AHK cân tại A ( vì AH = AK )
\(\Rightarrow\widehat{AHK}=\frac{180^0-\widehat{DAE}}{2}\left(2\right)\)
Từ (1) và (2) => D = AHK
mà 1 góc này ở vị trí đồng vị
=> HK // DE hay HK // BC ( đpcm )
Có j lên đây hỏi nha : Group Toán Học

Bạn tự vẽ hình nha![]()
AD = AB + BD
AE = AC + CE
mà AB = AC (tam giác ABC cân tại A)
BD = CE (gt)
=> AD = AE
HAE = HAB + BAE
KAD = KAC + CAD
mà HAB = KAC (tam giác AHB = tam giác AKC)
=> HAE = KAD
Xét tam giác AHE và tam giác AKD có:
AD = AE (chứng minh trên)
HAE = KAD (chứng minh trên)
AH = AK (tam giác AHB = tam giác AKC)
=> Tam giác AHE = Tam giác AKD (c.g.c)
Chúc bạn học tốt![]()