K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
1
SG
2
22 tháng 4 2017
Ta có:
a < b và 2 > 0 => 2a < 2b
a < b cộng hai vế với a
=> a + a < a + b => 2a < a + b
a < b và -1 < 0 => -a > -b
VK
22 tháng 4 2017
a) Từ a + 5 < b + 5
=> a + 5 + (-5) < b + 5 + (-5) (cộng hai vế với -5)
=> a < b
8 tháng 4 2021
a)từ a+5<b+5 ta cộng -5 vào 2 vế được a<b
b)từ -3a>-3b ta nhân 2 vế với -1/3 (tức là chia cả 2 vế cho -3) và -3a . -1/3< -3b . -1/3 sẽ được a<b
AH
Akai Haruma
Giáo viên
9 tháng 4 2018
Lời giải:
Áp dụng BĐT Cauchy-Schwarz:
\(B=\frac{1}{(a+2b)(a+2c)}+\frac{1}{(b+2a)(b+2c)}+\frac{1}{(c+2a)(c+2b)}\)
\(\geq \frac{9}{(a+2b)(a+2c)+(b+2a)(b+2c)+(c+2a)(c+2b)}\)
\(\Leftrightarrow B\geq \frac{9}{(a^2+2ac+2ab+4bc)+(b^2+2bc+2ab+4ac)+(c^2+2bc+2ac+4ab)}\)
\(\Leftrightarrow B\geq \frac{9}{a^2+b^2+c^2+8(ab+bc+ac)}=\frac{9}{(a+b+c)^2+6(ab+bc+ac)}(*)\)
Theo hệ quả quen thuộc của BĐT Cô-si:
\(a^2+b^2+c^2\geq ab+bc+ac\)
\(\Rightarrow (a+b+c)^2\geq 3(ab+bc+ac)\)
\(\Rightarrow 2(a+b+c)^2\geq 6(ab+bc+ac)(**)\)
Từ \((*); (**)\Rightarrow B\geq \frac{9}{(a+b+c)^2+2(a+b+c)^2}=\frac{3}{(a+b+c)^2}\geq \frac{3}{3^2}=\frac{1}{3}\)
(do \(a+b+c\leq 3)\)
Do đó: \(B_{\min}=\frac{1}{3}\)
Dấu bằng xảy ra khi \(a=b=c=1\)
NA
1
20 tháng 4 2020
1.Vì a < b nên a-b sẽ bằng một số nguyên âm.
Vậy a-b < 0.
2.Vì a < b nên 2a < 2b.
2a=a.a:nếu a+b=số nguyên dương thì 2a > a+b mà nếu a+b=số nguyên âm thì 2a > a+b.
2b=b.b:nếu a+b=số nguyên dương thì 2b > a+b mà nếu a+b=số nguyên âm thì 2b > a+b.
CM
5 tháng 6 2017
a < b
⇒ 2a < 2b (nhân hai vế với 2 > 0, BĐT không đổi chiều)
⇒ 2a + 1 < 2b + 1 (cộng hai vế với 1).
Vậy 2a + 1 < 2b + 1.
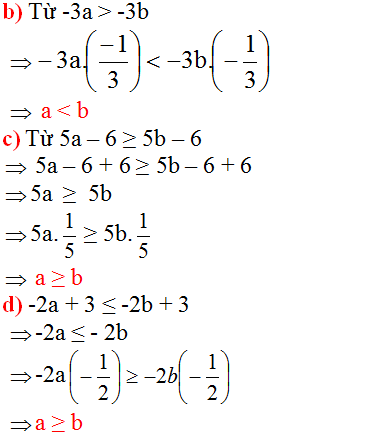
Tặng acc Online Math hơn 100 điểm hỏi đáp cho 50 thành viên đầu tiên !
Link nè : http://123link.vip/MlazJtj
Nhanh tay không hết ! Ưu đãi có hạn !
Buổi tối vui vẻ !
Chúc các bạn nhận acc thành công !
dễ mà ai chẳng làm đc anh