
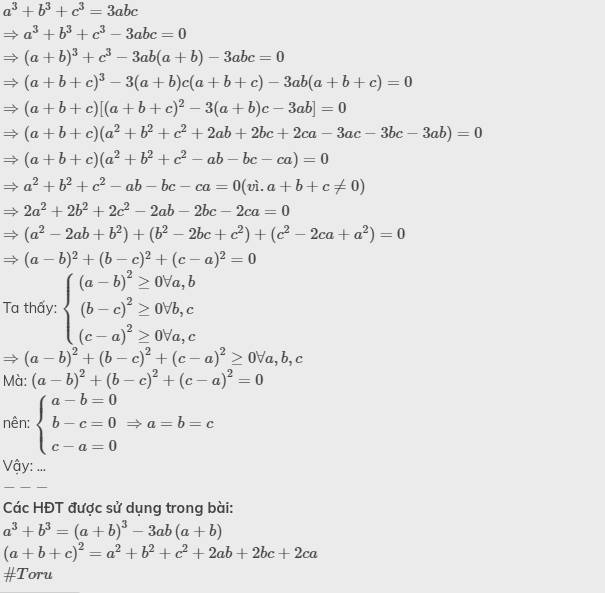
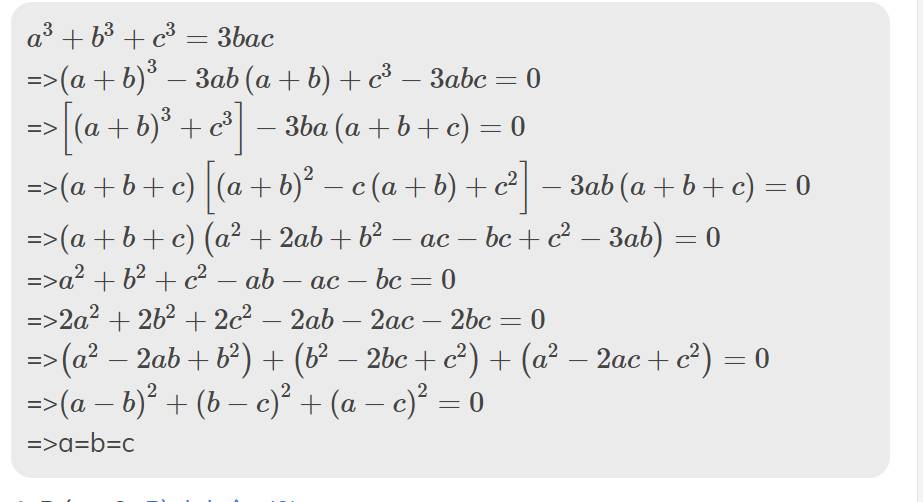
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

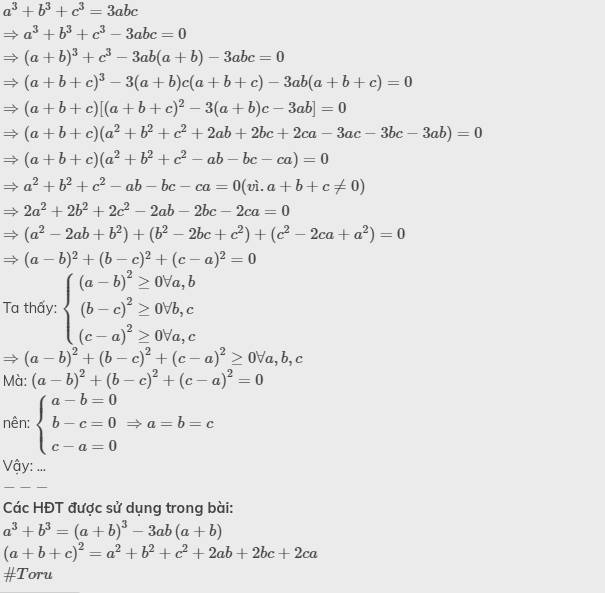
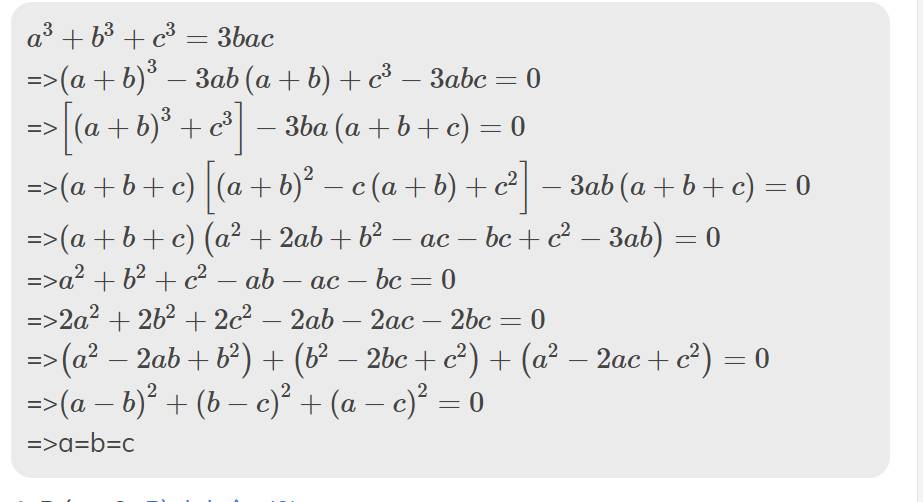

Ta có : \(a^3+b^3+c^3-3abc=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-c\right)\)
Do : \(a^3+b^3+c^3=3abc\) và \(a+b+c\ne0\) nên \(a^2+b^2+c^2-ab-bc-ac=0\)
Dễ dàng suy ra \(a=b=c\).Vậy \(N=\frac{3a^2}{\left(3a\right)^2}=\frac{1}{3}.\)

Mẫu của N phải là (a+b+c)^2013 chứ bạn
Đk để phân số tồn tại là : a+b+c khác 0
a^3+b^3+c^3=abc
<=> a^3+b^3+c^3-3abc = 0
<=> (a+b+c).(a^2+b^2+c^2-ab-bc-ca) = 0
<=> a^2+b^2+c^2-ab-bc-ca = 0 ( vì a+b+c khác 0 )
<=> 2a^2+2b^2+2c^2-2ab-2bc-2ca = 0
<=> (a^2-2ab+b^2)+(b^2-2bc+c^2)+(c^2-2ca+a^2) = 0
<=> (a-b)^2+(b-c)^2+(c-a)^2 = 0
<=> a-b=0 ; b-c=0 ; c-a=0
<=> a=b=c
Khi đó : N = 3a^2013/(3a)^2013 = 3/3^2013 = 1/3^2012
Tk mk nha

Ta có :
\(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)=0\)
Mà \(a+b+c\ne0\)
\(\Rightarrow a^2+b^2+c^2-ab-bc-ca=0\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Leftrightarrow a=b=c\)
\(\Rightarrow\frac{a^2+b^2+c^2}{\left(a+b+c\right)^2}=\frac{3a^2}{\left(3a\right)^2}=\frac{3a^2}{9a^2}=\frac{1}{3}\)

từ pt trên bạn pt đa thức thành nhân tử được (a+b+c)(a^2-ab+b^2-ac-bc+c^2)=0
mà a+b+c khác 0 nên a^2-ab+b^2-ac-bc+c^2=0
2(a^2-ab+b^2-ac-bc+c^2)=0
(a-b)^2+(a-c)^2+(b-c)^2=0
suy ra a=b=c
suy ra A=1/3

Ta có : \(a^3+b^3+c^3-3abc=0\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2+2ab-bc-ac\right)-3ab\left(a+b+c\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=0\)
\(\Leftrightarrow\frac{a+b+c}{2}\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]=0\)
Vì \(a+b+c\ne0\)nên \(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\Rightarrow a=b=c\)
Thay a = b = c vào biểu thức cần tính.

\(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)=0\)
\(\Leftrightarrow a^2+b^2+c^2-ab-bc-ca=0\)(vì \(a+b+c\ne0\))
\(\Leftrightarrow a^2+b^2+c^2=ab+bc+ca\)
\(N=\frac{a^2+b^2+c^2}{\left(a+b+c\right)^2}=\frac{a^2+b^2+c^2}{a^2+b^2+c^2+2ab+2bc+2ca}=\frac{a^2+b^2+c^2}{a^2+b^2+c^2+2\left(a^2+b^2+c^2\right)}=\frac{1}{3}\)

\(\left\{{}\begin{matrix}a^3+b^3+c^3=3abc\\a+b+c\ne0\end{matrix}\right.\) \(\Leftrightarrow a^2+b^2+c^2-\left(ab+bc+ca\right)=0\)
\(P=\dfrac{\left(a^2+b^2+c^2\right)^3}{\left(a+b+c\right)^6}=\left[\dfrac{a^2+b^2+c^2}{\left(a+b+c\right)^2}\right]^3=\left[\dfrac{\left(ab+bc+ca\right)}{3\left(ab+bc+ca\right)}\right]^3=\dfrac{1}{27}\)

a3 + b3 + c3 = 3abc
⇔ ( a3 + b3 ) + c3 - 3abc = 0
⇔ ( a + b )3 - 3ab( a + b ) + c3 - 3abc = 0
⇔ [ ( a + b )3 + c3 ] - [ 3ab( a + b ) + 3abc ] = 0
⇔ ( a + b + c )[ ( a + b )2 - ( a + b ).c + c2 ] - 3ab( a + b + c ) = 0
⇔ ( a + b + c )( a2 + 2ab + b2 - ac - bc + c2 - 3ab ) = 0
⇔ ( a + b + c )( a2 + b2 + c2 - ab - bc - ac ) = 0
⇔ \(\orbr{\begin{cases}a+b+c=0\\a^2+b^2+c^2-ab-bc-ac=0\end{cases}}\)
Từ đây tự làm tiếp nhé :))
Ta có : \(a^3+b^3+c^3=3abc\)
\(\Rightarrow a^3+b^3+c^3-3abc=0\)
\(\Rightarrow\left(a+b\right)^3-3ab\left(a+b\right)+c^3-3abc=0\)
\(\Rightarrow\left(a+b+c\right)^3-3\left(a+b\right)c\left(a+b+c\right)-3ab\left(a+b+c\right)=0\)
\(\Rightarrow\left(a+b+c\right)[\left(a+b+c\right)^2-3ac-3bc-3ab]=0\)
\(\Rightarrow\left(a+b+c\right)\left(a^2+b^2+c^2+2ab+2bc+2ac-3ab-3bc-3ac\right)=0\)
\(\Rightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=0\)
\(\Rightarrow\orbr{\begin{cases}a+b+c=0\\a^2+b^2+c^2-ab-bc-ac=0\end{cases}}\)
Để \(N\)có nghĩa thì \(\left(a+b+c\right)^2\ne0\)
Hay \(a+b+c\ne0\)
\(\Rightarrow a^2+b^2+c^2-ab-bc-ac=0\)
\(\Rightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac=0\)
\(\Rightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2\right)=0\)
\(\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
Vì \(\hept{\begin{cases}\left(a-b\right)^2\ge0\forall a,b\\\left(b-c\right)^2\ge0\forall b,c\\\left(c-a\right)^2\ge0\forall c,a\end{cases}}\)\(\Rightarrow\hept{\begin{cases}\left(a-b\right)^2=0\\\left(b-c\right)^2=0\\\left(c-a\right)^2=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}a-b=0\\b-c=0\\c-a=0\end{cases}}\)\(\Rightarrow a=b=c\)
Thay \(a=b=c\)vào \(N\), ta có : \(N=\frac{3a^2}{\left(3a\right)^2}=\frac{3a^2}{9a^2}=\frac{1}{3}\)
Vậy \(N=\frac{1}{3}\)