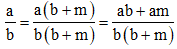Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{a}{b}>1\Rightarrow a>b>m\)
Ta có:
\(\frac{a-m}{b-m}=\frac{ab-bm}{\left(b-m\right).b}\)
\(\frac{a}{b}=\frac{ab-am}{\left(b-m\right).b}\)
\(am>bm\left(a>b\right)\)
\(\Rightarrow ab-bm>ab-am\)
\(\Rightarrow\frac{a-m}{b-m}>\frac{a}{b}\left(1\right)\)
\(\frac{a+m}{b+m}=\frac{ab+bm}{\left(b+m\right).b}\)
\(\frac{a}{b}=\frac{ab+am}{\left(b+m\right).b}\)
\(bm< am\left(b< a\right)\)
\(\Rightarrow ab+bm< ab+am\)
\(\Rightarrow\frac{a+m}{b+m}< \frac{a}{b}\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow\frac{a-m}{b-m}>\frac{a}{b}>\frac{a+m}{b+m}\)
+ Do a/b > 1
=> a > b
=> a.m > b.m
=> a.b - a.m < a.b - b.m
=> a.(b - m) < b.(a - m)
=> a/b < a-m/b-m (1)
Do a/b > 1
=> a > b
=> a.m > b.m
=> a.m + a.b > b.m + a.b
=> a.(b + m) > b.(a + m)
=> a/b > a+m/b+m (2)
Từ (1) và (2) => a-m/b-m > a/b > a+m/b+m
Ủng hộ mk nha ☆_☆^_-

TA co a/b=a.(b+m)/b.(b+m)=a.b+a.m/b.b+b.m
Ta lai co a+m/b+m=b.(a+m)/b.(b+m)=a.b+b.m/b.b+b.m.Suy ra a.b+a.m/b.b+b.m<a.b+b.m/b.b+b.m=a.m<b.m
VI 0<a<b nen a/b<a=m/b=m

Ta có:
\(1-\frac{-2015}{-2016}=1-\frac{2015}{2016}=\frac{1}{2016}\)
\(1-\frac{-2016}{-2017}=1-\frac{2016}{2017}=\frac{1}{2017}\)
Vì \(\frac{1}{2016}>\frac{1}{2017}\Rightarrow\frac{-2015}{-2016}< \frac{-2016}{-2017}\)
Đây là cách so sánh phần bù, bạn có thể lên mạng tham khảo thêm nhé :)

Ta có:
\(\frac{a}{b}=\frac{a\times\left(b+m\right)}{b\times\left(b+m\right)}=\frac{a\times b+a\times m}{b\times b+b\times m}\)
\(\frac{a+m}{b+m}=\frac{\left(a+m\right)\times b}{\left(b+m\right)\times b}=\frac{a\times b+m\times b}{b\times b+b\times m}\)
vì \(\frac{a}{b}>1\) nên \(a>b\), ta suy ra \(a\times m>b\times m\)
hay \(a\times b+a\times m>a\times b+m\times b\)
hay \(\frac{a\times b+a\times m}{b\times b+b\times m}>\frac{a\times b+m\times b}{b\times b+b\times m}\)
hay \(\frac{a}{b}>\frac{a+m}{b+m}\)
Vì \(\frac{a}{b}>1\)
=> a > b
=> a.m > b.m
=> a.m + a.b > b.m + a.b
=> a.(b + m) > b.(a + m)
=> \(\frac{a}{b}>\frac{a+m}{b+m}\)

Lời giải:
Bổ sung điều kiện $a,b$ là số tự nhiên.
$\frac{a}{b}-\frac{a+m}{b+m}=\frac{a(b+m)-b(a+m)}{b(b+m)}$
$=\frac{m(a-b)}{b(b+m)}$
$=\frac{m}{b+m}.(\frac{a}{b}-1)>0$ do $\frac{a}{b}>1$ và $\frac{m}{b+m}>0$ với $m,b$ tự nhiên.
$\Rightarrow \frac{a}{b}> \frac{a+m}{b+m}$

Cùng bớt cả tử và mẫu đi m đơn vị(m>0) thì phân số mới nhỏ hơn phân số đã cho
Chứng minh: Nếu a/b nhỏ hơn 1 thì a/b > a-m/b-m ( 0<a<b;m>0)
Do a < b
=> am < bm
=> ab - am > ab - bm
=> a.( b - m) > b.( a - m)
=> a/b > a-m/b-m
Vậy cùng bớt cả tử và mẫu đi m đơn vị(m>0) thì phân số mới nhỏ hơn phân số đã cho
Phân số mới là: \(\frac{a-m}{b-m}\)
Ta đi so sánh \(\frac{a}{b}\)và \(\frac{a-m}{b-m}\)
Ta có:0<a<b
a.(b-m)=ab-am
b(a-m)=ba-bm
=>a.(b-m)>b.(a-m)
Vậy phân số mới bé hơn phân số đã cho

Bài làm:
a) Vì \(\frac{13}{15}< 1\)\(\Rightarrow\frac{13}{15}< \frac{13+11}{15+11}=\frac{24}{26}\)
b) Vì \(\frac{13}{15}< 1\)\(\Rightarrow\frac{13}{15}< \frac{13+10}{15+10}=\frac{23}{25}\)
c) Vì \(\frac{3}{5}< 1\)\(\Rightarrow\frac{3}{5}< \frac{3+30}{5+30}=\frac{33}{35}\)
Học tốt!!!!
1 lớp học có 2 học sinh một bạn bị chết hỏi còn bao nhiêu bạn