Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Vecto pháp tuyến

Một điểm trên giao tuyến là K(0;-2;0)
Phương trình tham số của
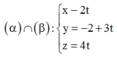
Gọi I là trung điểm của MN, ta có I(2;3;3)
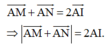
vậy A M → + A N → nhỏ nhất khi AI nhỏ nhất
Mà A ∈ α ∩ β nên AI nhỏ nhất khi A I ⊥ α ∩ β
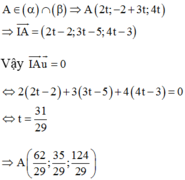

Đáp án B
Mặt phẳng (α) song song với mặt phẳng (β) khi và chỉ khi:
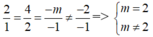
Hệ này vô nghiệm nên không có giá trị của m thỏa mãn.


N' đối xứng với N qua đường thẳng d nên K là trung điểm của NN'
Vậy N' có tọa độ 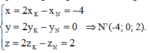




Gọi \(M\left(x;y;0\right)\) \(\Rightarrow OM^2=x^2+y^2\)
\(d^2\left(M;\left(\alpha\right)\right)=\frac{\left(x+2y+4\right)^2}{9}\) ; \(d^2\left(M;\left(\beta\right)\right)=\frac{\left(2x-2y-13\right)^2}{9}\)
\(\left(x+2y+4\right)^2=\left(2x-2y-13\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2y+4=2x-2y-13\\x+2y+4=-2x+2y+13\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4y+17\\3x=9\Rightarrow x=3\end{matrix}\right.\)
Th1: \(\left\{{}\begin{matrix}x=3\\x^2+y^2=\frac{\left(x+2y+4\right)^2}{9}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=3\\9y^2+81=4y^2+28y+49\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\5y^2-28y+32=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(3;4;0\right)\\M\left(3;\frac{8}{5};0\right)\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}x=4y+17\\x^2+y^2=\frac{\left(x+2y+4\right)^2}{9}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4y+17\\\left(4y+17\right)^2+y^2=\left(2y+7\right)^2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=4y+17\\13y^2+108y+240=0\end{matrix}\right.\) (vô nghiệm)
Bạn kiểm tra lại tính toán