Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(AB^2 + AC^2 = 25^2 = 625\)
\(AD^2 + 81 = AB^2\)
\(AD^2 + 256 = AC^2\)
\(=> AD^2 + 81 + AD^2 + 256 = 625\)
=> \(2AD^2 = 288\)
=> \(AD^2 = 144\)
=> AD = 12(cm)
=>\( AB^2 = 9^2 + 12^2 = 225\)
=> AB = 15 (cm)
=> \(AC^2 = 12^2 + 16^2 = 400\)
=> AC = 20(cm)
và BC = 25(cm)

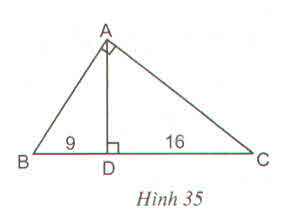
Ta có: \(BC=BD+DC=9+16=25\left(cm\right)\)
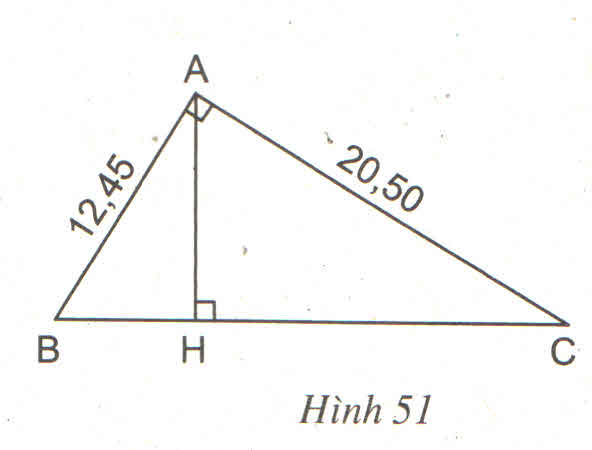
Xét \(\Delta DBA\) và \(\Delta ABC\):
\(\widehat{A}=\widehat{D}\left(=90^o\right)\)
\(\widehat{B}=\widehat{A_2}\)(cùng phụ với góc\(A_1\))
\(\Rightarrow\Delta DBA\)~\(\Delta ABC\)
\(\Rightarrow\dfrac{DB}{AB}=\dfrac{AB}{BC}\Leftrightarrow AB^2=DB.BC=9.25=225\Rightarrow AB=15\left(cm\right)\)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC, có:
\(AB^2+AC^2=BC^2\Leftrightarrow15^2+AC^2=25^2\Rightarrow AC=\sqrt{25^2-15^2}=20\)
Vậy các cạnh của tam giác vuông ABC lần lượt là: \(15;20;25\)

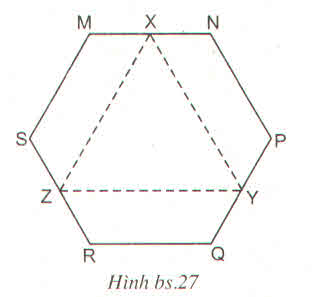
a) Đáy của hình lăng trụ đứng là một tam giác vuông cân
b) Các mặt bên nhận được không phải tất cả là hình vuông
\(\Bigg(\) hai hình vuông và một hình chữ nhật \(\Bigg)\)

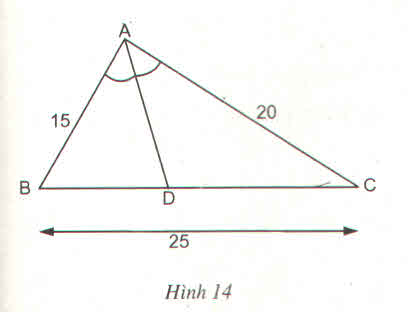
Trong ΔABC, ta có: AD là đường phân giác của (BAC)
Suy ra: \(\frac{DB}{DC}=\frac{AB}{AC}\)(tính chất đường phân giác)
Mà AB = 15 (cm); AC = 20 (cm)
Nên \(\frac{DB}{DC}=\frac{15}{20}\)
uy ra: \(\frac{DB}{DB+DC}=\frac{15}{15+20}\)(tính chất tỉ lệ thức)
Suy ra: \(\frac{DB}{BC}=\frac{15}{35}\Rightarrow DB=\frac{15}{35}.BC=\frac{15}{35}.25=\frac{75}{7}cm\)
\(\Rightarrow DC=BC-BD=25-\frac{75}{7}=\frac{100}{7}cm\)
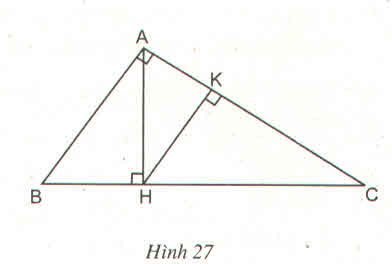
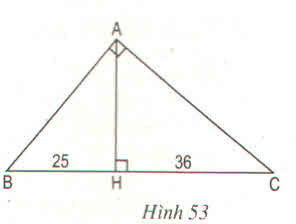
b. Kẻ AH ⊥ BC
Ta có: SABD = 1/2 AH.BD; SADC = 1/2 AH.DC
Suy ra :\(\frac{S_{ABD}}{S_{ADC}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.DC}=\frac{BD}{DC}\)
Mà\(\frac{DB}{DC}=\frac{15}{20}=\frac{3}{4}\)
\(\Rightarrow\frac{S_{ABD}}{S_{ADC}}=\frac{3}{4}\)

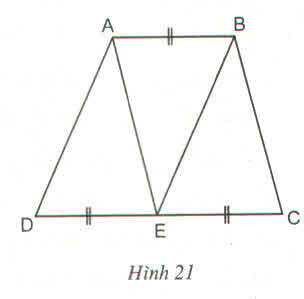
Xét tứ giác ABED có:
AB//DE;AB=DE
=>ABED là hình bình hành ( một cặp cạnh vừa song song vừa bằng nhau)
nên AD=BE
Xét tam giác EDA và tam giác ABE có:
AB=DE (gt)
AE là cạnh chung
AD=BE ( vừa chứng minh)
=>tam giác EDA =tam giác ABE
<=>tam giác EDA đồng dạng với tam giác ABE (1)
Xét tứ giác ABCE có:
AB//EC;AB=EC
=>ABCE là hình bình hành (một cặp cạnh vừa song song vừa bằng nhau
=>AE=BC
Xét tam giác ABE và tam giác CEB có:
AB=EC(gt)
BE là cạnh chung
AE=BC (vừa chứng minh)
=>tam giác ABE=tam giác CEB
<=>tam giác ABE đồng dạng với tam giác CEB (2)
từ (1) và (2)
=>tam giác EDA đồng dạng với tam giác ABE và đồng dang với tam giác CEB.
Ai biết cách vẽ kí hiệu đồng dạng không chỉ mình cách vẽ với cảm mơn bạn nhiều.





Chọn phương án (C): Tam giác đều