Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đặt góc IAD là D1; góc IDC là D2; góc CDL là D3
a) Ta có D1+D2=90độ
D2+D3=90độ
=>D1=D3
xét 2tam giác vuông IAD và DCL
Có D1=D3(CM trên)
AD=DC(cạnh hình vuông)
=> tam giác IAD=tam giác LCD(góc nhọn-cạnh góc vuông)
=>DL=DI
=> tam giác IDL cân tại D
b) xét tam giác vuông KDL có
DC là đường cao
=> 1/DC^2=(1/DK^2)+(1/DL^2) (1)
Mà DL=DI (2)
mà DC không đổi (3)
Từ (1),(2) và (3) =>DPCM

Bạn tự vẽ hình nha
a) xét \(\Delta\)ADI và \(\Delta\)CDL có:
^DAI=^DIL=90(gt)
AD=DC(gt)
^ADI=^CDL(cùng phụ với ^IDC)
=> \(\Delta\)ADI=\(\Delta\)CDL(g.c.g)
=> DI=DL
=> \(\Delta\)DIL cân tại A
b) Ta có: \(\frac{1}{DI^2}+\frac{1}{DK^2}=\frac{1}{DL^2}+\frac{1}{DK^2}\)(vì DI=DK)
Xét \(\Delta\)DKL vuông tại D(gt) có DC là đường cao
=> \(\frac{1}{DL^2}+\frac{1}{DK^2}=\frac{1}{DC^2}\)(theo hệ thức liên hệ tới đường cao)
Mà DC không đổi
=>\(\frac{1}{DC^2}\)không đổi
Vậy \(\frac{1}{DL^2}+\frac{1}{DK^2}\)không đổi hay \(\frac{1}{DI^2}+\frac{1}{DK^2}\)không đổi khi I chuyển đọng trên AB
(chú ý: ^ nghĩa là góc)


a) ΔADI và ΔCDL có: góc A = góc C = 90°
AD = CD (hai cạnh hình vuông)
góc D1 = góc D2
cùng phụ với góc CDI
Do đó ΔADI = ΔCDL (g.c.g)
Suy ra DI = DL. Vậy ΔDIL cân
b) Áp dụng hệ thức  là không đổi.
là không đổi.
Nhận xét: Câu a) chỉ là gợi ý để làm câu b). Điều phải chứng minh ở câu b) rất gần với hệ thức 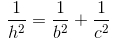
Nếu đề bài không cho vẽ DL ⊥ DK thì ta vẫn phải vẽ đường phụ DL ⊥ DK để có thể vận dụng hệ thức trên.
