K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

26 tháng 5 2017

b) Ta có ACC' là tam giác vuông có cạnh \(AC=a\sqrt{2},CC'=a\)
Vậy \(AC'^2=AC^2+CC^2\Rightarrow AC'^2=2a^2+a^2=3a^2\)
Vậy \(AC'=a\sqrt{3}\)

CM
23 tháng 6 2019
Chọn A
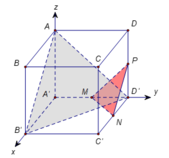
Đối với những bài cồng kềnh và tính toán rất phức tạp
thế này thì nên tọa độ hóa giải rất nhanh, khỏi phải mất nhiều
thời gian và tư duy. Gắn trục tọa độ Oxyz như hình vẽ bên với
A'(0;0;0), D(0;5;6), C' (4;5;0)
![]()
![]()
![]()
![]()
![]()
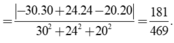


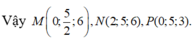
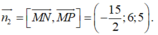
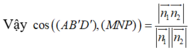
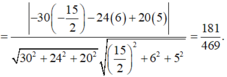
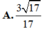
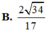
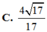
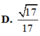

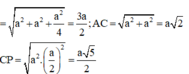
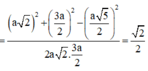
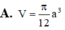
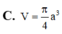
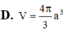

Lời giải:
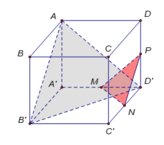
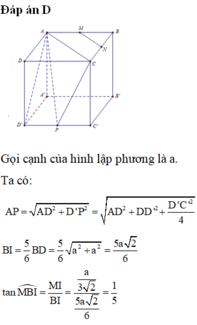
Gọi cạnh hình lập phương là $a$.
Vì $AD\parallel A'D'$ nên:
$\angle (A'D', C'D)=\angle (AD, C'D)=\widehat{ADC'}$
Ta thấy:
$AD=a$
$DC'=\sqrt{DD'^2+D'C'^2}=\sqrt{a^2+a^2}=\sqrt{2}a$
$AC'=\sqrt{AA'^2+A'C'^2}=\sqrt{a^2+2a^2}=\sqrt{3}a$
$\Rightarrow AD^2+DC'^2=AC'^2$
$\Rightarrow ADC'$ là tam giác vuông tại $D$ (theo định lý Pitago đảo)
$\Rightarrow \angle (A'D', C'D)=\widehat{ADC'}=90^0$