Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

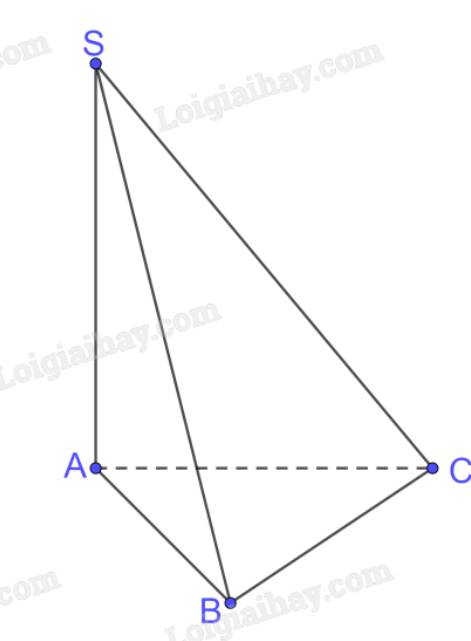
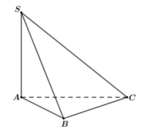
a) Ta có SA \( \bot \) (ABC) nên A là hình chiếu của S trên (ABC)
b) A là hình chiếu của S trên (ABC)
B là hình chiếu của B trên (ABC)
C là hình chiếu của C trên (ABC)
\( \Rightarrow \) Tam giác ABC là hình chiếu của tam giác SBC.
c) B là hình chiếu của C trên (SAB)
S, B là hình chiếu của chính nó trên (SAB)
\( \Rightarrow \) SB là hình chiếu của tam giác SBC trên (SAB)

a.
Do \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp SB\)
b.
\(SA\perp\left(ABC\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABC)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABC)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)

Chọn C
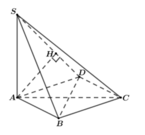
Xác định được
![]()
Khi đó ta tính được
![]()
Trong mặt phẳng (ABC) lấy điểm D sao cho ABCD là hình chữ nhật => AB//(SCD) nên
![]()
![]()
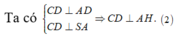
Từ (1) và (2) suy ra
![]()
Xét tam giác vuông SAD có
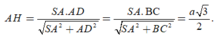
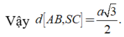
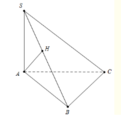
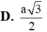

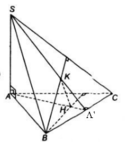


a) Trong (SAB) kẻ \(AD \bot SB\) tại D.
\(\left. \begin{array}{l}BC \bot AD\\SB \bot AD\\BC \cap SB = \left\{ B \right\}\end{array} \right\} \Rightarrow AD \bot \left( {SBC} \right) \Rightarrow \)D là hình chiếu của A trên (SBC).
b) A là hình chiếu của S trên (ABC) \(\left( {SA \bot \left( {ABC} \right)} \right)\)
C là hình chiếu của C trên (ABC)
\( \Rightarrow \) AC là hình chiếu của SC trên (ABC)
\( \Rightarrow \) \(\left( {SC,\left( {ABC} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
Xét tam giác ABC vuông tại B có
\(A{C^2} = A{B^2} + B{C^2} = 2{a^2} \Rightarrow AC = a\sqrt 2 \)
Xét tam giác SAC vuông tại A có
\(\tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }} \Rightarrow \widehat {SCA} = \arctan \frac{1}{{\sqrt 2 }}\)
Vậy \(\left( {SC,\left( {ABCD} \right)} \right) = \arctan \frac{1}{{\sqrt 2 }}\)