


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.






a) (SAD) ∩ (SBC) = SE
b) Trong (SBE): MN ∩ SE = F
Trong (SAE): AF ∩ SD = P là điểm cần tìm
c) Thiết diện là tứ giác AMNP
TenAnh1 A = (-0.14, -7.4) A = (-0.14, -7.4) A = (-0.14, -7.4) B = (14.46, -7.36) B = (14.46, -7.36) B = (14.46, -7.36) C = (-3.74, -5.6) C = (-3.74, -5.6) C = (-3.74, -5.6) D = (11.62, -5.6) D = (11.62, -5.6) D = (11.62, -5.6)

S A B C D M N O G K H P Q
a/
Ta có
\(S\in\left(SAC\right);S\in\left(SBD\right)\)
Trong mp (ABCD) gọi O là giao của AC và BD
\(O\in AC\Rightarrow O\in\left(SAC\right);O\in BD\Rightarrow O\in\left(SBD\right)\)
\(\Rightarrow SO\in\left(SAC\right)\) và \(SO\in\left(SBD\right)\) => SO là giao tuyến của (SAC) và (SBD)
b/
Trong mp (ABCD) Từ G dựng đường thẳng // AC cắt BC tại K
Xét tg SAC có
SM=AM (gt); SN=CN (gt) => MN là đường trung bình của tg SAC
=> MN//AC
Mà GM//AC
=> MN//GK mà \(G\in\left(GMN\right)\Rightarrow GK\in\left(GMN\right)\) (Từ 1 điểm trong mặt phẳng chỉ dựng được duy nhất 1 đường thẳng thuộc mặt phẳng đó và // với 1 đường thẳng cho trươc thuộc mặt phẳng)
\(\Rightarrow K\in\left(GMN\right);K\in BC\) => K llaf giao của BC với (GMN)
c/
Ta có
\(KN\in\left(GMN\right);KN\in\left(SBC\right)\) => KN là giao tuyến của (GMN) với (SBC)
Trong (ABCD) KG cắt AB tại H
\(KG\in\left(GMN\right)\Rightarrow KH\in\left(GMN\right)\)
\(KG\in\left(ABCD\right)\Rightarrow KH\in\left(ABCD\right)\)
=> KH là giao tuyến của (GMN) với (ABCD)
Ta có
\(HM\in\left(SAB\right);HM\in\left(GMN\right)\) => HM là giao tuyến của (GMN) với (SAB)
Trong mp(SAC) gọi P là giao của SO với MN
\(P\in MN\Rightarrow P\in\left(GMN\right)\)
Trong mp(SBD) Nối G với P cắt SD tại Q
\(\Rightarrow GP\in\left(GMN\right)\Rightarrow Q\in GMN\)
\(\Rightarrow MQ\in\left(GMN\right)\) mà \(MQ\in\left(SAD\right)\) => MQ là giao tuyến của (GMN) với (SAD)
Ta có
\(NQ\in\left(GMN\right);NQ\in\left(SCD\right)\) => NQ là giao tuyến của (GMN) với (SCD)
=> thiết diện của hình chóp bị cắt bởi (GMN) là đa giác HMQNK

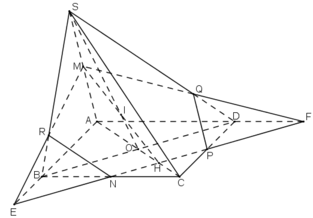
a) Tìm thiết diện :
Trong mp(ABCD), gọi F = AD ∩ PN và E = AB ∩ PN
Trong mp(SAD), gọi Q = MF ∩ SD
Trong mp(SAB), gọi R = ME ∩ SB
Nối PQ, NR ta được các đoạn giao tuyến của mp(MNP) với các mặt bên và mặt đáy của hình chóp là MQ, QP, PN, NR, RM
Vậy thiết diện cắt bởi mặt phẳng (MNP) là ngũ giác MQPNR.
b) Tìm SO ∩ (MNP). Gọi H là giao điểm của AC và PN .
Trong (SAC), SO ∩ MH = I
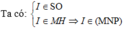
Vậy I = SO ∩ (MNP).

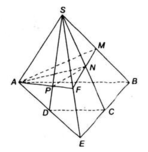
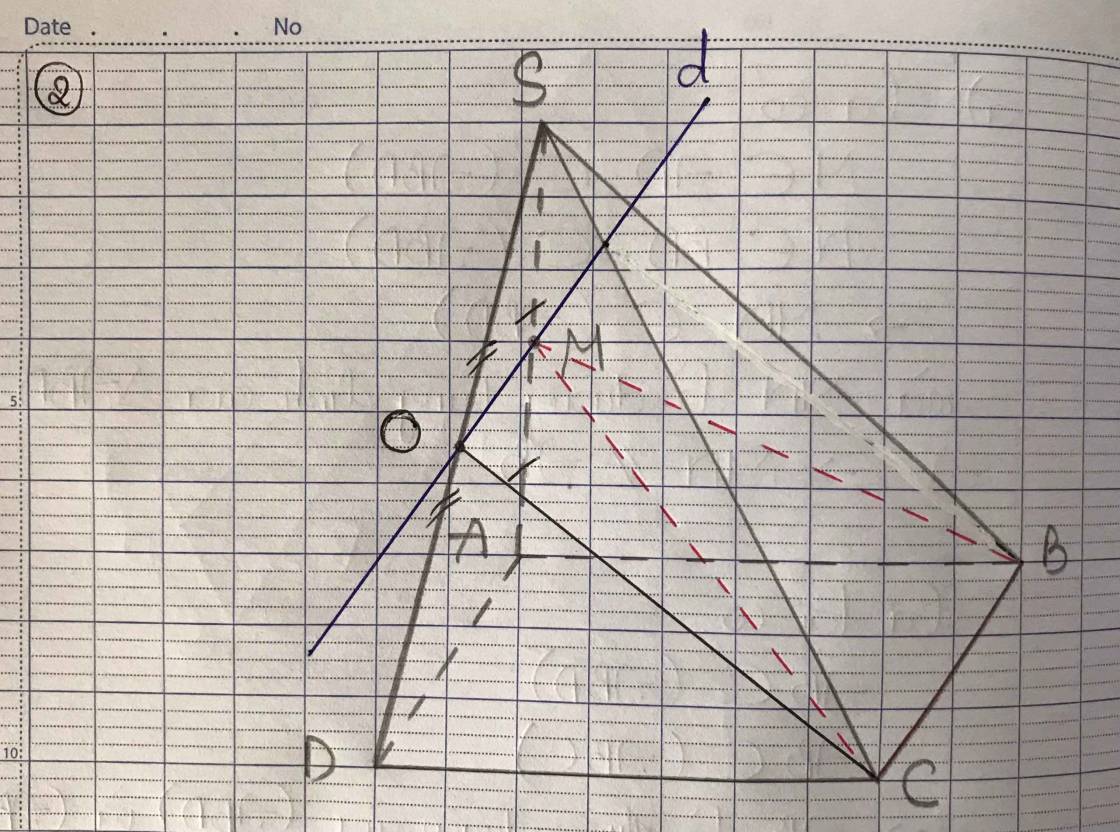
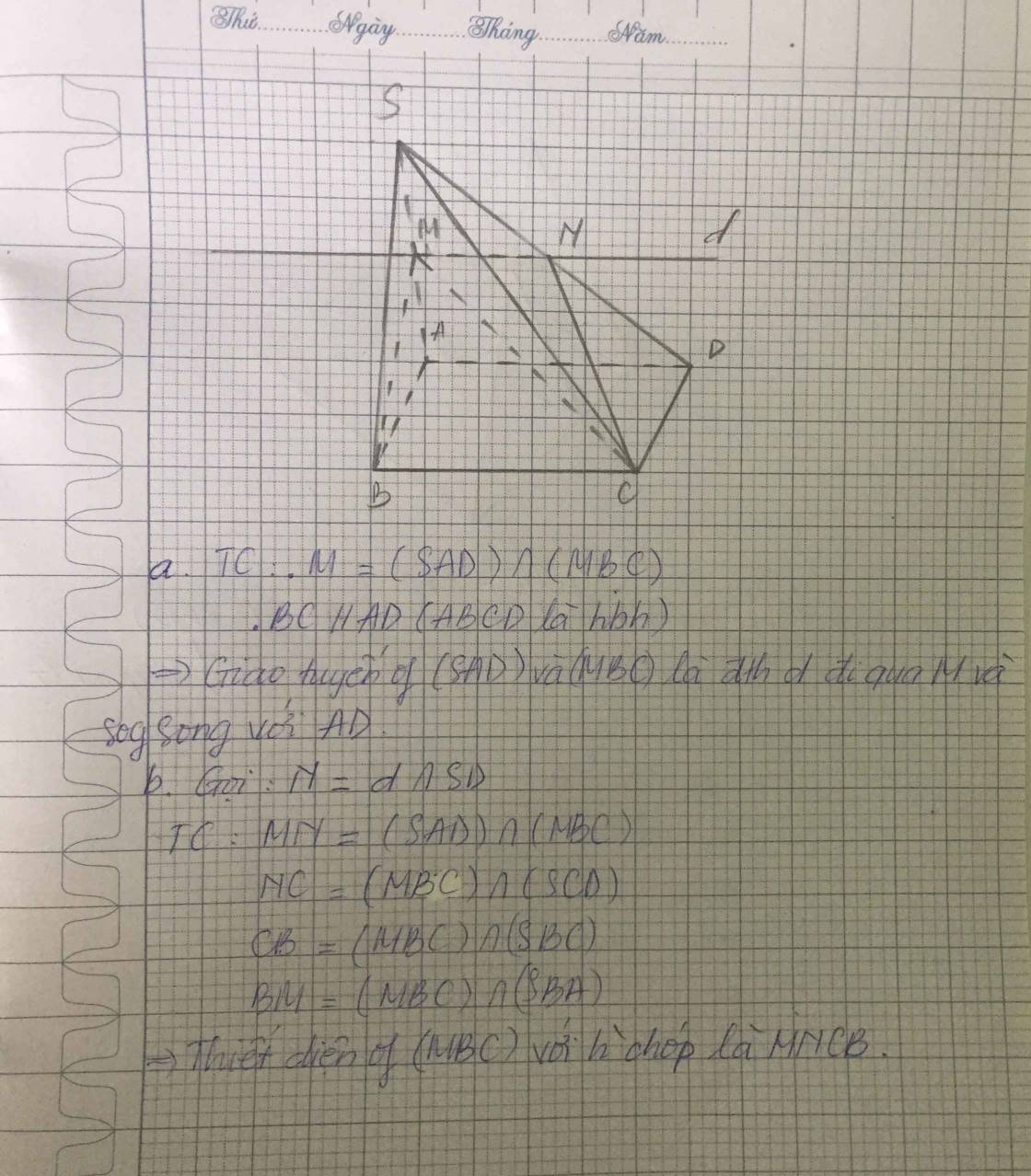
a) Tìm (SAD) ∩ (SBC)
Gọi E= AD ∩ BC. Ta có:
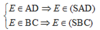
Do đó E ∈ (SAD) ∩ (SBC).
mà S ∈ (SAD) ∩ (SBC).
⇒ SE = (SAD) ∩ (SBC)
b) Tìm SD ∩ (AMN)
+ Tìm giao tuyến của (SAD) và (AMN) :
Trong mp (SBE), gọi F = MN ∩ SE :
F ∈ SE ⊂ (SAD) ⇒ F ∈ (SAD)
F ∈ MN ⊂ (AMN) ⇒ F ∈ (AMN)
⇒ F ∈ (SAD) ∩ (AMN)
⇒ AF = (SAD) ∩ (AMN).
+ Trong mp (SAD), gọi AF ∩ SD = P
⇒ P = SD ∩ (AMN).
c) Tìm thiết diện với mp(AMN):
(AMN) ∩ (SAB) = AM;
(AMN) ∩ (SBC) = MN;
(AMN) ∩ (SCD) = NP
(AMN) ∩ (SAD) = PA.
⇒ Thiết diện cần tìm là tứ giác AMNP.

a: Chọn mp(SBD) có chứa BM
\(O\in BD\subset\left(SBD\right);O\in AC\subset\left(SAC\right)\)
Do đó: \(O\in\left(SBD\right)\cap\left(SAC\right)\)
mà \(S\in\left(SBD\right)\cap\left(SAC\right)\)
nên \(\left(SBD\right)\cap\left(SAC\right)=SO\)
Gọi E là giao điểm của SO với BM
=>E là giao điểm của BM với mp(SAC)
b: \(M\in SD\subset\left(SAD\right);M\in\left(MAC\right)\)
=>\(M\in\left(SAD\right)\cap\left(MAC\right)\)
mà \(A\in\left(MAC\right)\cap\left(SAD\right)\)
nên \(\left(MAC\right)\cap\left(SAD\right)=AM\)

Qua S kẻ đường thẳng d song song AD (và BC)
Do \(\left\{{}\begin{matrix}S\in\left(SAD\right)\cap\left(SBC\right)\\AD||BC\\AD\in\left(SAD\right)\\BC\in\left(SBC\right)\end{matrix}\right.\) \(\Rightarrow\) giao tuyến của (SAD) và (SBC) là đường thẳng qua S và song song AD, BC
\(\Rightarrow d=\left(SAD\right)\cap\left(SBC\right)\)

a.
Trong mp (ABCD), kéo dài AD và BC cắt nhau tại E
\(\left\{{}\begin{matrix}E\in AD\in\left(SAD\right)\\E\in BC\in\left(SBC\right)\end{matrix}\right.\) \(\Rightarrow E\in\left(SAD\right)\cap\left(SBC\right)\)
\(\Rightarrow SE=\left(SAD\right)\cap\left(SBC\right)\)
b.
Gọi O là giao điểm AC và BD \(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
Trong mp (SBD), nối DM cắt SO tại I
\(\left\{{}\begin{matrix}I\in SO\in\left(SAC\right)\\I\in DM\end{matrix}\right.\)
\(\Rightarrow I=DM\cap\left(SAC\right)\)
c.
Gọi F là trung điểm SA \(\Rightarrow FM\) là đường trung bình tam giác SAB
\(\Rightarrow FM||AB\Rightarrow FM||CD\)
Mà \(M\in\left(MCD\right)\Rightarrow F\in\left(MCD\right)\)
\(\Rightarrow\) Tứ giác CDFM là thiết diện của (MCD) và chóp

a.
Nối BN kéo dài cắt AD tại E
\(\left\{{}\begin{matrix}E\in\left(BMN\right)\\E\in\left(SAD\right)\end{matrix}\right.\) \(\Rightarrow E=\left(BMN\right)\cap\left(SAD\right)\)
\(\left\{{}\begin{matrix}M\in SA\in\left(SAD\right)\\M\in\left(BMN\right)\end{matrix}\right.\) \(\Rightarrow M=\left(BMN\right)\cap\left(SAD\right)\)
\(\Rightarrow EM=\left(BMN\right)\cap\left(SAD\right)\)
b.
Gọi F là giao điểm EM và SD
Trong mp (SCD), nối FN kéo dài cắt SC kéo dài tại G
\(\Rightarrow G=SC\cap\left(BMN\right)\)