Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Trên cạnh SB, SC lần lượt lấy các điểm M, N thỏa mãn SM = SN = 1.
Ta có AM = 1, AN = 2 , MN = 3
=> tam giác AMN vuông tại A
Hình chóp S.AMN có SA = SM = SN = 1.
=> hình chiếu của S trên (AMN) là tâm I của đường tròn ngoại tiếp tam giác AMN, ta có I là trung điểm của MN
Trong
∆
SIM,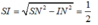 
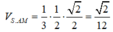
Ta có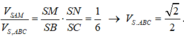 
+)Gọi H là chân đường cao hạ từ A - -> BC
Tam giác AHC vuông tại H nên
AH = √(a² -a²/4) = a√3/2
Diện tích tam giác ABC là S(ABC) = 1/2.AH.BC= 1/2.a²√3/2
(dvdt)
+)Từ S hạ SK ┴ AH , Kết hợp AH ┴ BC ta có SK ┴ (ABC)
Hay SK là đường cao của hình chóp đều SABC
+) Bài cho góc giữa các mặt bên với đáy là 60 độ nên
góc giữa (SH,HK) = 60 độ
Tam giác vuông SKH có SK = HK.tan(60)
Tam giác vuông BKH có HK = a/2.tan(30) = a√3/6
- - > SK = a√3/6.tan(60) = a/2
Vậy V(SABC) =1/3.SK.S(ABC) = 1/3.a/2.1/2.a²√3/2
= a³√3/24 (dvtt)
Chọn đáp án B.
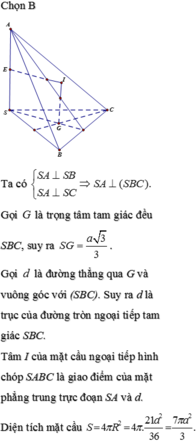
Ta có: S A ⊥ S B S A ⊥ S C ⇒ S A ⊥ ( S B C )
Vì vậy áp dụng công thức cho trường hợp khối chóp có cạnh bên vuông góc đáy có:
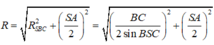
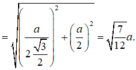
cho hình chóp S.ABC, có góc ASB=ASC=BSC=60 độ, SA=3, SB=6, SC=9. Tính khoảng cách d từ C đến mp(SAB)
Chọn điểm B' và C' lần lượt thuộc SB và SC sao ctho SA=SB'=SC'=3
Thấy ngay các tam giác SAB', SB'C', SAC', AB'C' đều
suy ra tứ diện SAB'C' là tứ diện đều, cạnh bằng 3
Dễ dàng tính được \(V_{SAB'C'}=\frac{9\sqrt{2}}{4}\)
Dùng tỷ lệ thể tích: \(\frac{V_{S.ABC}}{V_{S.AB'C'}}=\frac{SA}{SA}\cdot\frac{SB}{SB'}\cdot\frac{SC}{SC'}=1\cdot\frac{6}{3}\cdot\frac{9}{3}=6\Rightarrow V_{S.ABC}=\frac{27\sqrt{3}}{2}\)
\(S_{SAB}=\frac{1}{2}.SA.SB.sin\widehat{ASB}=\frac{9\sqrt{3}}{2}\)
\(\Rightarrow d\left(C;\left(SAB\right)\right)=\frac{3V_{S.ABC}}{S_{SAB}}=9\)
Phương pháp:
+) Lấy 
sao cho SA = SB' = SC' = 2a. Chóp có các cạnh bên bằng nhau có chân đường cao trùng với tâm đường tròn ngoại tiếp đáy.
+) Tính thể tích 
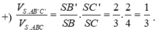Tính thể tích
V
S
.
A
B
C
Cách giải:
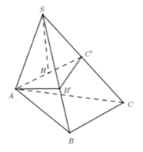
Lấy 
sao cho SA = SB' = SC' = 2a.
là tam giác đều cạnh 2a.
=> AB' = B'C' = 2a
Xét tam giác vuông SAC' có: 
Xét tam giác AB'C' có: 
Do đó tam giác AB'C' vuông tại B' (Định lí Pytago đảo).
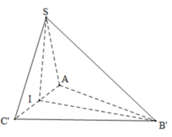
Gọi H là trung điểm của AC' => H là tâm đường tròn ngoại tiếp 
Ta có 
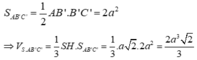
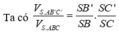
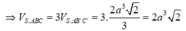
Chọn: C
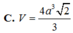
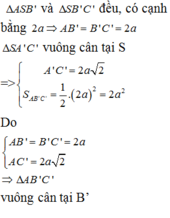
Công thức tính nhanh thể tích tứ diện khi biết các góc tại 1 đỉnh:
\(V=\frac{SA.SB.SC}{6}\sqrt{1+2cos\widehat{ASB}.cos\widehat{BSC}.cos\widehat{CSA}-cos^2\widehat{ASB}-cos^2\widehat{BSC}-cos^2\widehat{CSA}}\)
\(=\frac{6}{6}\sqrt{1+2.\frac{1}{2}.\left(-\frac{1}{2}\right).0-\left(\frac{1}{2}\right)^2-\left(-\frac{1}{2}\right)^2}=\frac{\sqrt{2}}{2}\)