Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)
\(=\overrightarrow{AB}+k\overrightarrow{BC}\)
\(=\overrightarrow{AB}+k\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
\(=\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\)
b) \(\overrightarrow{NP}=\overrightarrow{AP}-\overrightarrow{AN}\)
\(=\dfrac{2}{3}\overrightarrow{AC}-\dfrac{3}{4}\overrightarrow{AB}\)
Để \(AM\perp NP\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{NP}=\overrightarrow{0}\)
\(\Rightarrow\left[\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\right]\left(-\dfrac{3}{4}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\dfrac{3\left(k-1\right)}{4}AB^2+\dfrac{2k}{3}AC^2+\dfrac{2\left(1-k\right)}{3}\overrightarrow{AB}.\overrightarrow{AC}-\dfrac{3k}{4}\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{0}\)
\(\Leftrightarrow\dfrac{3\left(k-1\right)}{4}AB^2+\dfrac{2k}{3}AB^2+\dfrac{1-k}{3}AB^2-\dfrac{3k}{8}AB^2=0\)
\(\Leftrightarrow AB^2\left[\dfrac{3\left(k-1\right)}{4}+\dfrac{2k}{3}+\dfrac{1-k}{3}-\dfrac{3k}{8}\right]=0\)
\(\Leftrightarrow18\left(k-1\right)+16k+8\left(1-k\right)-9k=0\left(AB>0\right)\)
\(\Leftrightarrow17k=10\)
\(\Leftrightarrow k=\dfrac{10}{17}\)

1.
\(\left\{{}\begin{matrix}\overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BN}\\\overrightarrow{CA}+\overrightarrow{CB}=2\overrightarrow{CP}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-\overrightarrow{AB}+\overrightarrow{BC}=2\overrightarrow{BN}\\\overrightarrow{CB}+\overrightarrow{BA}+\overrightarrow{CB}=2\overrightarrow{CP}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{AB}-\overrightarrow{BC}=-2\overrightarrow{BN}\\\overrightarrow{AB}+2\overrightarrow{BC}=-2\overrightarrow{CP}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\overrightarrow{AB}-2\overrightarrow{BC}=-4\overrightarrow{BN}\\\overrightarrow{AB}+2\overrightarrow{BC}=-2\overrightarrow{CP}\end{matrix}\right.\)
\(\Rightarrow3\overrightarrow{AB}=-4\overrightarrow{BN}-2\overrightarrow{CP}\Rightarrow\overrightarrow{AB}=-\frac{4}{3}\overrightarrow{BN}-\frac{2}{3}\overrightarrow{CP}\)
2.
\(\overrightarrow{BI}=\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{DI}\)
\(=-\overrightarrow{AB}+\overrightarrow{AD}+\frac{1}{2}\overrightarrow{DC}\)
\(=-\overrightarrow{AB}+\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}\)
\(\Rightarrow\overrightarrow{BI}=-\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}\)
\(\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{BG}=\overrightarrow{AB}+\frac{1}{3}\left(\overrightarrow{BI}+\overrightarrow{BC}\right)\)
\(=\overrightarrow{AB}+\frac{1}{3}\left(-\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AD}\right)\)
\(=\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AG}=\frac{5}{6}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}\)

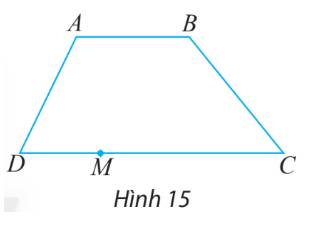
a) ABCD là hình thang nên AB//CD
Các vectơ cùng hướng với vectơ \(\overrightarrow {AB} \) là các vectơ có hướng từ trái qua phải nên đó là: \(\overrightarrow {DC} ,\overrightarrow {DM} ,\overrightarrow {MC} \)
b) \(\overrightarrow {DM} \)có hướng từ trái sang phải nên các vectơ ngược hướng với vectơ \(\overrightarrow {DM} \)là \(\overrightarrow {BA} ,\overrightarrow {MD} ,\overrightarrow {CM} ,\overrightarrow {CD} \)

\(\overrightarrow{AB}=3\overrightarrow{AM};\overrightarrow{CD}=2\overrightarrow{CN};\overrightarrow{BI}=\frac{6}{11}\overrightarrow{BC}\)
Có tứ giác ABCD là hbh=> \(\overrightarrow{CD}=\overrightarrow{BA}\Rightarrow\overrightarrow{BA}=2\overrightarrow{CN}\)
Có G là trọng tâm tam giác BMN
\(\Rightarrow\overrightarrow{GB}+\overrightarrow{GM}+\overrightarrow{GN}=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{GA}+\overrightarrow{AB}+\overrightarrow{AN}+\overrightarrow{AM}=\overrightarrow{0}\)\(\Leftrightarrow3\overrightarrow{GA}+\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{CN}+\frac{1}{3}\overrightarrow{AB}=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{GA}+\frac{4}{3}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BA}+\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{AG}=\frac{-11}{6}\overrightarrow{AB}-\overrightarrow{AD}\Leftrightarrow\overrightarrow{AG}=\frac{-11}{18}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AD}\)
Có \(\overrightarrow{AN}=\overrightarrow{AC}+\overrightarrow{CN}=\frac{1}{2}\overrightarrow{BA}+\overrightarrow{AB}+\overrightarrow{AD}=\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}\)
b/ \(\overrightarrow{AG}=\frac{-11}{18}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AD}\)
\(\overrightarrow{AI}=\overrightarrow{AB}+\overrightarrow{BI}=\overrightarrow{AB}+\frac{6}{11}\overrightarrow{BC}=\overrightarrow{AB}+\frac{6}{11}\overrightarrow{AD}\)
Có \(\overrightarrow{AG}=-\frac{11}{18}\overrightarrow{AI}\Rightarrow\) thẳng hàng
Tính AG còn sai, mà AG=-AI vẫn bảo thẳng hàng. Không biết làm thì đừng thể hiện

xét tứ giác AECF: có AE = FC và AE//FC => AECF là hình bình hành => AF//CE
xét △DNC: có F là trung điểm của DC và FM//CN (đường tb) => M là trung điểm của DN => vtDM = vtMN (1)
xét △BMA: có E là trung điểm của AB và NE//AM ( đường tb) => N là trung điểm của MB => BM=MN (2)
từ (1) và (2) suy ra : DM=MN=NB => vtDM = vtMN = vtNB ( cùng hướng, cùng độ lớn)
A B C D E M N F
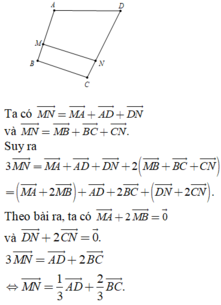

vecto AN=vecto AC+vecto CN
=vecto AC+1/2vecto CD
=vecto AC+1/2vecto BA
=vecto AC-1/2vecto AB