Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Vì $a+b\geq 1\Rightarrow b\geq 1-a; a\geq 1-b$. Do đó:
\(A\geq \frac{8a^2+1-a}{4a}+b^2=2a+\frac{1}{4a}-\frac{1}{4}+b^2\)
\(\geq a+1-b+\frac{1}{4a}-\frac{1}{4}+b^2=\left(a+\frac{1}{4a}\right)+(b^2-b+\frac{1}{4})+\frac{1}{2}\)
Áp dụng BĐT AM-GM: \(a+\frac{1}{4a}\geq 1\)
$b^2-b+\frac{1}{4}=(b-\frac{1}{2})^2\geq 0$
Do đó: $A\geq 1+0+\frac{1}{2}=\frac{3}{2}$
Vậy $A_{\min}=\frac{3}{2}$. Dấu "=" xảy ra khi $a=b=\frac{1}{2}$


\(A=2a+\frac{b}{4a}+b^2=a+a+\frac{b}{4a}+b^2\)
\(A\ge a+1-b+\frac{1-a}{4a}+b^2\)
\(A\ge a+\frac{1}{4a}+b^2-b=a+\frac{1}{4a}+\left(b-\frac{1}{2}\right)^2-\frac{1}{4}\)
\(A\ge a+\frac{1}{4a}-\frac{1}{4}\ge2\sqrt{\frac{a}{4a}}-\frac{1}{4}=\frac{1}{4}\)
\(A_{min}=\frac{1}{4}\) khi \(\left\{{}\begin{matrix}a=\frac{1}{2}\\b=\frac{1}{2}\end{matrix}\right.\)

Tìm min:
Theo BĐT AM-GM thì: P=a2+b2+c2≥ab+bc+acP=a2+b2+c2≥ab+bc+ac hay P≥9P≥9
Vậy Pmin=9Pmin=9. Giá trị này đạt tại a=b=c=√3a=b=c=3
-----------
Tìm max:
P=a2+b2+c2=(a+b+c)2−2(ab+bc+ac)=(a+b+c)2−18P=a2+b2+c2=(a+b+c)2−2(ab+bc+ac)=(a+b+c)2−18
Vì a,b,c≥1a,b,c≥1 nên:
(a−1)(b−1)≥0⇔ab+1≥a+b(a−1)(b−1)≥0⇔ab+1≥a+b
Hoàn toàn tương tự: bc+1≥b+c;ac+1≥a+cbc+1≥b+c;ac+1≥a+c
Cộng lại: 2(a+b+c)≤ab+bc+ac+3=122(a+b+c)≤ab+bc+ac+3=12
⇒a+b+c≤6⇒a+b+c≤6
⇒P=(a+b+c)2−18≤62−18=18⇒P=(a+b+c)2−18≤62−18=18
Vậy Pmax=18Pmax=18. Giá trị này đạt tại (a,b,c)=(1,1,4)(a,b,c)=(1,1,4) và hoán vị
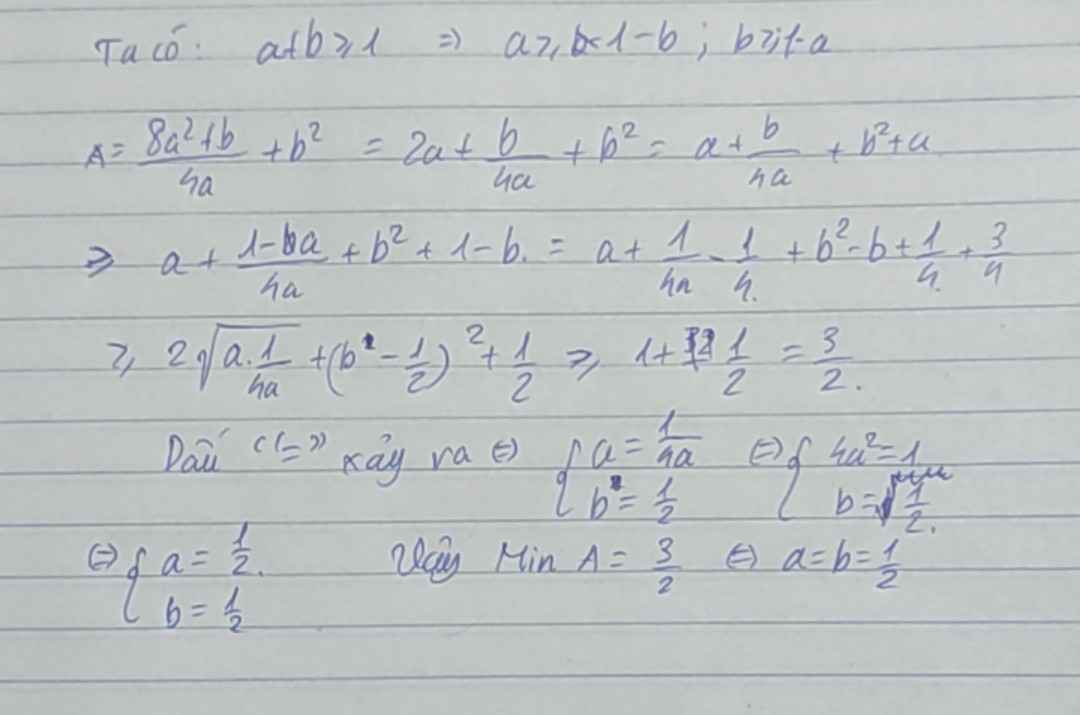
\(\frac{8a^2+b}{4a}+b^2=2a+\frac{b}{4a}+b^2=a+a+\frac{b}{4a}+b^2\)
\(\ge a+1-b+\frac{1-a}{4a}+b^2=a+1-b+\frac{1}{4a}-\frac{1}{4}+b^2\)(do \(a+b\ge1\))
\(=\left(a+\frac{1}{4a}\right)+b^2-b+\frac{1}{4}+\frac{1}{2}\)
\(\ge2\sqrt{a\cdot\frac{1}{4a}}+\left(b-\frac{1}{2}\right)^2+\frac{1}{2}\)
\(\ge2\cdot\frac{1}{2}+\frac{1}{2}=\frac{3}{2}\)
Dấu = khi \(a=b=\frac{1}{2}\)