Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

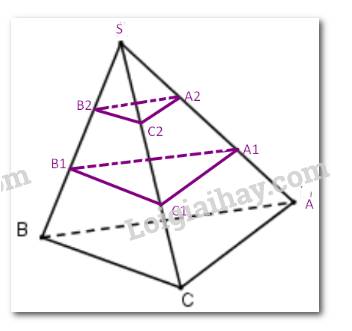
Áp dụng định lí Thales cho ba mặt phẳng (ABC), (P), (Q) và hai cát tuyến SA, SC ta có:
\(\frac{{{C_2}S}}{{{A_2}S}} = \frac{{{C_1}{C_2}}}{{{A_1}{A_{2\;}}}} = \frac{{C{C_1}}}{{A{A_1}}}\) mà \(A{A_1} = {A_1}{A_2} = {A_2}S\).
Suy ra \(C{C_1} = {C_1}{C_2} = {C_2}S\).
Áp dụng định lí Thales cho ba mặt phẳng (ABC), (P), (Q) và hai cát tuyến SA, SB ta có:
\(\frac{{{B_2}S}}{{{A_2}S}} = \frac{{{B_1}{B_2}}}{{{A_1}{A_2}}} = \frac{{B{B_1}}}{{A{A_1}}}\) mà \(A{A_1} = A{A_2} = {A_2}S\).
Suy ra \(B{B_1} = {B_1}{B_2} = {B_2}S\).

a) Chứng minh B 1 , C 1 , D 1 lần lượt là trung điểm của các cạnh SB, SC, SD
Ta có:
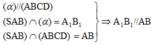
⇒ A 1 B 1 là đường trung bình của tam giác SAB.
⇒ B 1 là trung điểm của SB (đpcm)
*Chứng minh tương tự ta cũng được:
• C 1 là trung điểm của SC.
• D 1 là trung điểm của SD.
b) Chứng minh B 1 B 2 = B 2 B , C 1 C 2 = C 2 C , D 1 D 2 = D 2 D .
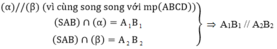
⇒ A 2 B 2 là đường trung bình của hình thang A 1 B 1 B A
⇒ B 2 là trung điểm của B 1 B
⇒ B 1 B 2 = B 2 B (đpcm)
*Chứng minh tương tự ta cũng được:
• C 2 là trung điểm của C 1 C 2 ⇒ C 1 C 2 = C 2 C
• D 2 là trung điểm của D 1 D 2 ⇒ D 1 D 2 = D 2 D .
c) Các hình chóp cụt có một đáy là tứ giác ABCD, đó là : A 1 B 1 C 1 D 1 . A B C D v à A 2 B 2 C 2 D 2 . A B C D

a) Vì mặt phẳng không đi qua S và song song với mặt phẳng đáy, cắt các cạnh SA1, SA2,.... SAn, tương ứng tại B1, B2,..., Bn nên theo định lý Talet trong từng tam giác SA1A2, …, SAn-1An thì \(\frac{{S{B_1}}}{{S{A_1}}} = \frac{{S{B_2}}}{{S{A_2}}} = \frac{{{B_1}{B_2}}}{{{A_1}{A_2}}} = ... = \frac{{S{B_n}}}{{S{A_n}}}\) mà S.A1A2...An là hình chóp đều nên S.B1B2...Bn cũng là một hình chóp đều.
b) Ta có \(SH \bot \left( {{A_1}{A_2}...{A_n}} \right)\) (H là tâm của đa giác A1A2...An)
Mà \(\left( {{A_1}{A_2}...{A_n}} \right)//\left( {{B_1}{B_2}...{B_n}} \right)\)
\( \Rightarrow \)\(SH \bot \left( {{B_1}{B_2}...{B_n}} \right)\)
Mà \(SK \bot \left( {{B_1}{B_2}...{B_n}} \right)\) (K là tâm của đa giác B1B2...Bn)
\( \Rightarrow \) SH trùng SK
Vậy đường thẳng SH đi qua tâm K của đa giác đều B1B2...Bn, và HK vuông góc với các mặt phẳng (A1A2...An), (B1B2...Bn)

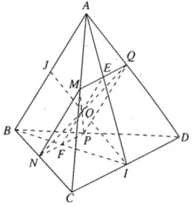
a) 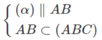
⇒ (α) ∩ (ABC) = MN và MN // AB
Ta có N ∈ (BCD) và 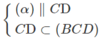
Nên ⇒ (α) ∩ (BCD) = NP và NP // CD
Ta có P ∈ (ABD)
Và 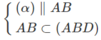 nên ⇒ (α) ∩ (ABD) = PQ và PQ // AB
nên ⇒ (α) ∩ (ABD) = PQ và PQ // AB
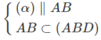 nên ⇒ (α) ∩ (ACD) = MQ và MQ // CD
nên ⇒ (α) ∩ (ACD) = MQ và MQ // CD
Do đó MN // PQ và NP // MQ, Vậy tứ giác MNPQ là hình bình hành.
b) Ta có: MP ∩ NQ = O. Gọi I là trung điểm của CD.
Trong tam giác ACD có : MQ // CD ⇒ AI cắt MQ tại trung điểm E của MQ.
Trong tam giác ACD có : NP // CD ⇒ BI cắt NP tại trung điểm F của NP.
Vì MNPQ là hình bình hành nên ta có
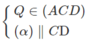
EF // MN ⇒ EF // AB
Trong ΔABI ta có EF // AB suy ra : IO cắt AB tại trung điểm J
⇒ I, O, J thẳng hàng
⇒ O ∈ IJ cố định.
Vì M di động trên đoạn AC nên Ochạy trong đoạn IJ .
Vậy tập hợp các điểm O là đoạn IJ.

a) Ta có: a // a’ mà a’ ⊂ (Q) nên a // (Q);
b // b’ mà b’ ⊂ (Q) nên b // (Q).
Do a // (Q);
b // (Q);
a, b cắt nhau tại M và cùng nằm trong mặt phẳng (P)
Suy ra (P) // (Q).
b) Do (R) // (Q) nên trong mp(R) tồn tại hai đường thẳng a’’, b’’ đi qua M và lần lượt song song với a’, b’ trong mp(Q).
Ta có: a // a’, a’’ // a’ nên a // a’’.
Mà a’’ ∈ (R), do đó a // (R)
Do hai mặt phẳng (P) và (R) có một điểm chung nên chúng có đường thẳng chung d.
Ta có: a // (R);
a ⊂ (P);
(P) ∩ (R) = d.
Suy ra a // d.
Mà a, d cùng nằm trong mặt phẳng (P) và cùng đi qua điểm M nên đường thẳng a chính là giao tuyến của hai mặt phẳng (P) và (R).
Chứng minh tương tự ta cũng có đường thằng b cũng là giao tuyến của hai mặt phẳng (P) và (R).
Như vậy, hai mặt phẳng (P) và (R) có hai giao tuyến a và b nên (P) và (R) là hai mặt phẳng trùng nhau.

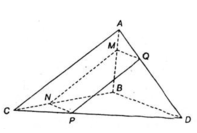
a) + (α) // AC
⇒ Giao tuyến của (α) và (ABC) là đường thẳng song song với AC.
Mà M ∈ (ABC) ∩ (α).
⇒ (ABC) ∩ (α) = MN là đường thẳng qua M, song song với AC (N ∈ BC).
+ Tương tự (α) ∩ (ABD) = MQ là đường thẳng qua M song song với BD (Q ∈ AD).
+ (α) ∩ (BCD) = NP là đường thẳng qua N song song với BD (P ∈ CD).
+ (α) ∩ (ACD) = QP.
b)Ta có:
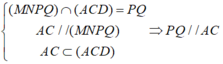
Suy ra, tứ giác MNPQ có các cạnh đối song song với nhau nên tứ giác MNPQ là hình bình hành.

Đáp án B
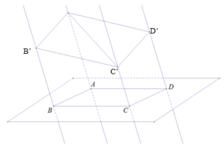
Giả sử mặt phẳng ban đầu là (A’B’C’). Ta cần xác định điểm D sao cho
Xét (A’B’C’) và (C’CD) có:
C’ là điểm chung
A’B’//(C’CD) (do (A’B’BA) // (C’CD))
⇒ giao tuyến của (A’B’C’) và (C’CD) là đường thẳng m đi qua điểm C’ và song song với A’B’
⇒ m cắt d tại D’ là điểm cần tìm
Xét hình A’B’C’D’ có A’B’ // C’D’
⇒ A’B’ = C’D’ ( a, b, c, d là các đường thẳng song song lần lượt đi qua A, B, C, D là các đỉnh của hình bình hành)
⇒ A’B’C’D’ là hình bình hành

Gọi N, P, Q lần lượt là trung điểm AC, AD, BD thì dễ dàng chứng minh hình thoi MNPQ là thiết diện (việc chứng minh thiết diện là hình thoi cũng vô cùng dễ dàng, 4 cái đường trung bình)
Mặt khác tứ diện đều nên các cặp cạnh đối vuông góc
\(\left\{{}\begin{matrix}AB\perp CD\\AB||MN\\CD||NP\end{matrix}\right.\) \(\Rightarrow MN\perp NP\)
\(\Rightarrow\) Thiết diện là hình vuông cạnh \(\dfrac{a}{2}\)
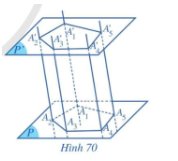
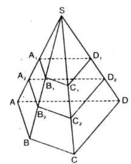



a: là những hình bình hành
b: song song và bằng nhau