Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}m-3+n=-3\\-2m+n+6=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m+n=0\\-2m+n=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3m=3\\m+n=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=1\\n=-1\end{matrix}\right.\)

d: Để (d)//\(y=\dfrac{-2x-1}{5}=\dfrac{-2}{5}x-\dfrac{1}{5}\) thì
\(\left\{{}\begin{matrix}m-3=\dfrac{-2}{5}\\n\ne-\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{13}{5}\\n\ne-\dfrac{1}{5}\end{matrix}\right.\)

Bài 1:
Gọi giao điểm của 2 đths là \(I(x_I,y_I)\)
a)
Giao điểm nằm trên trục tung thì \(x_I=0\)
Ta có: \(I\in (d);(d')\Rightarrow \left\{\begin{matrix} y_I=m.0-4=-4\\ y_I=0+m=m\end{matrix}\right.\)
\(\Rightarrow m=-4\)
b) Giao điểm nằm trên trục hoành thì \(y_I=0\)
Ta có: \(I\in (d);(d')\Rightarrow \left\{\begin{matrix} 0=mx_I-4\\ 0=x_I+m\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} mx_I=4\\ x_I=-m\end{matrix}\right.\)
\(\Rightarrow -m^2=4\) (VL)
Vậy k tồn tại $m$ để hai đths cắt nhau tại một điểm trên trục hoành.
c)
Hai đths cắt nhau tại điểm có tung độ bằng $1$
\(\Leftrightarrow \left\{\begin{matrix} mx_I-4=1\\ x_I+m=1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} mx_I=5\\ x_I=1-m\end{matrix}\right.\)
\(\Rightarrow m(1-m)=5\)
\(\Leftrightarrow (m-\frac{1}{2})^2+\frac{19}{4}=0\) (VL)
Vậy k tồn tại $m$ để 2 đths cắt nhau tại điểm có tung độ bằng $1$
Bài 2:
\(y=(m+1)x-m-3, \forall m\)
\(\Leftrightarrow m(x-1)+x-3-y=0, \forall m\)
Để điều này xảy ra thì \(\left\{\begin{matrix} x-1=0\\ x-3-y=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=1\\ y=-2\end{matrix}\right.\)
Như vậy $(d)$ luôn đi qua điểm \((1,-2)\) với mọi $m$
b) ĐK: \(m\neq -1\)
\(A=(d)\cap Ox\Rightarrow \left\{\begin{matrix} y_A=0\\ y_A=(m+1)x_A-m-3\end{matrix}\right. \)
\(\Rightarrow \left\{\begin{matrix} y_A=0\\ x_A=\frac{m+3}{m+1}\end{matrix}\right.\)
\(B=(d)\cap Oy\Rightarrow \left\{\begin{matrix} x_B=0\\ y_B=(m+1)x_B-m-3\end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} x_B=0\\ y_B=-m-3\end{matrix}\right.\)
Vì $A,B$ nằm trên trục hoành và trục tung nên hiển nhiên tam giác $OAB$ vuông sẵn. Vậy để nó là tam giác vuông cân thì $OA=OB$
\(\Leftrightarrow \sqrt{(\frac{m+3}{m+1})^2}=\sqrt{(-m-3)^2}\)
\(\Leftrightarrow (\frac{m+3}{m+1})^2=(m+3)^2\)
\(\Leftrightarrow (m+3)^2\left(\frac{1}{(m+1)^2}-1\right)=0\)
\(\Rightarrow \left[\begin{matrix} m=-3\\ m=-2\\ m=0\end{matrix}\right.\)
Với $m=-3$ thì $A,B$ trùng nhau nên $m=0,-2$

a, Biến đổi hệ phương trình ban đầu ta được hệ x - y = 0 3 x + 3 y = 12
Từ đó tìm được x = 2, y = 2
b, Phương trình hoành độ giao điểm của d và (p):
x 2 - 2 x - m 2 + 2 m = 0 (1)
d cắt (P) tại hai điểm phân biệt nằm về hai phía của trục tung Oy <=> (1) có hai nghiệm trái dấu. Từ đó tìm được 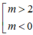
Kết luận 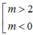
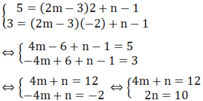
c) (d) cắt (d') tại 1 điểm nằm trên trục tung khi