Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

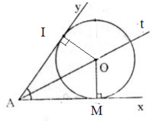
Gọi O là tâm của một đường tròn bất kì tiếp xúc với hai cạnh góc xAy. Theo tính chất của hai tiếp tuyến cắt nhau ta có:
![]()
Hay AO là tia phân giác của góc xAy.
Vậy tâm các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên tia phân giác của góc xAy.

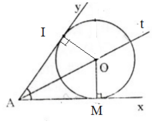
Gọi O là tâm của một đường tròn bất kì tiếp xúc với hai cạnh góc xAy. Theo tính chất của hai tiếp tuyến cắt nhau ta có:
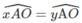
Hay AO là tia phân giác của góc xAy.
Vậy tâm các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên tia phân giác của góc xAy.

Gọi O là tâm của một đường tròn bất kì tiếp xúc với hai cạnh góc xAy. Theo tính chất của hai tiếp tuyến cắt nhau ta có:
ˆxAO=ˆyAOxAO^=yAO^
Hay AO là tia phân giác của góc xAy. Vậy tâm O các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên tia phân giác của góc(xAy).

Câu 3: Tâm của đường tròn ( O) tiếp xúc với 2 cạnh đường Ay , Ax nằm trên đường phân giác OA


Cách dựng:
– Dựng tia phân giác At của góc xAy
– Dựng đường thẳng Bz qua B và vuông góc với tia Ax
– Giao điểm O của At và Bz là tâm của đường tròn cần dựng.
– Dựng đường tròn tâm O, bán kính R = OB, ta được đường tròn cần dựng.

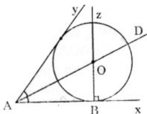
Đường tròn (O) tiếp xúc với hai tia Ax và Ay nên tâm O của (O) nằm trên tia phân giác của góc xAy

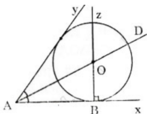
Đường tròn (O) tiếp xúc với hai tia Ax và Ay nên tâm O của (O) nằm trên tia phân giác của góc xAy. (Xem lại Bài 28 trang 116 SGK Toán 9 Tập 1) . Do đó ta có cách dựng:
- Dựng tia phân giác At của góc xAy.
- Dựng đường thẳng Bz qua B và vuông góc với tia Ax.
- Giao điểm O của At và Bz là tâm của đường tròn cần dựng.
- Dựng đường tròn tâm O, bán kính R = OB, ta được đường tròn cần dựng.

* Phân tích
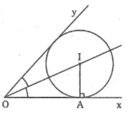
Giả sử đường tròn (I) dựng được thỏa mãn điều kiện bài toán
- Đường tròn (I) tiếp xúc với Ox và Oy nên điểm I nằm trên tia phân giác của góc xOy
- Đường tròn (I) tiếp xúc với Ox tại A nên I nằm trên đường vuông góc với Ox kẻ từ A
Vậy I là giao điểm của tia phân giác góc xOy và đường thẳng vuông góc với Ox tại A
* Cách dựng
- Dựng tia phân giác của góc xOy
- Dựng đường thẳng vuông góc với Ox tại A cắt tia phân giác của góc xOy tại I
- Dựng đường tròn (I; IA)
* Chứng minh
Ta có: Ox ⊥ IA tại A nên Ox là tiếp tuyến của (I)
I nằm trên tia phân giác của góc xOy nên I cách đều hai cạnh Ox, Oy. Khi đó khoảng cách từ I đến Oy bằng IA nên Oy cũng là tiếp tuyến của đường tròn (I).
Vậy đường tròn (I) đi qua A và tiếp xúc với hai cạnh của góc xOy.
* Biện luận
Vì góc xOy nhỏ hơn 180 ° nên góc tạo bởi một cạnh của góc với tia phân giác là góc nhọn. Khi đó đường thẳng vuông góc với Ox tại A luôn cắt tia phân giác của góc xOy.