Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B O M H I K E N
1) Ta thấy: Tứ giác AHMB nội tiếp đường tròn => ^HAM=^HBM; ^HMA=^HBA
Do H là điểm chính giữa của cung AM nên \(\Delta\)AHM cân tại H => ^HAM=^HMA
Từ đó suy ra: ^HBM=^HBA hay ^HBE=^HBA => BH là phân giác ^ABE
H thuộc nửa đường tròn đường kính AB => AH\(\perp\)BH hay BH\(\perp\)AE
Xét \(\Delta\)BAE: BH là phân giác ^ABE; BH\(\perp\)AE => \(\Delta\)BAE cân đỉnh B (đpcm).
2) Xét \(\Delta\)KHA và \(\Delta\)KAB: ^KHA=^KAB (=900); ^AKB chung => \(\Delta\)KHA ~ \(\Delta\)KAB (g.g)
\(\Rightarrow\frac{KH}{KA}=\frac{KA}{KB}\Rightarrow KH.KB=KA^2\)(1)
Ta có: AE\(\perp\)BK tại H và AH=EH => A đối xứng với E qua BK => AK=KE. Thay vào (1):
\(\Rightarrow KH.KB=KE^2\)(đpcm).
3) Dễ thấy: 2 điểm A và N cùng nằm trên (B) => BA=BN => \(\Delta\)ABN cân đỉnh B
Mà BM\(\perp\)AN => BM là đường trung trực của AN hay BE là trung trực của AN
=> EA=EN => \(\Delta\)AEN cân đỉnh E = >^EAN=^ENA (2)
Lại có: ^HAM=^HBM (Cùng chắn cung HM) hay ^EAN=^EBI (3)
(2); (3) => ^ENA=^EBI hay ^ENI=^EBI => Tứ giác BIEN nội tiếp đường tròn (đpcm).
4) Ta có: ^KAB=900. Mà KA và AB đều cố định
Vậy để ^KAM=900 thì điểm M phải trùng với điểm B.

1)Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)
~~~~~~~~~ Bài làm ~~~~~~~~~
A B C O I K H Q D
Ta có: \(\widehat{HBD}=\widehat{DAC}\) (Cùng phụ với \(\widehat{ACB}\))
\(\widehat{KBD}=\widehat{DAC}\)( Góc nối tiếp cùng chắn cung \(KC\))
\(\Rightarrow\widehat{HBD}=\widehat{KBD}\)
Ta lại có: \(BD\perp HK\)
\(\Rightarrow BD\) là đường trung trực của \(HK\)
\(\Rightarrow\Delta IHK\) cân tại \(I\)
\(\Rightarrow\widehat{BKD}=\widehat{BHD}=\widehat{AHQ}\)
Lại có:\(\widehat{DKO}=\widehat{HAO}\)( \(\Delta OKA\) cân tại \(O\))
Vì vậy: \(\widehat{DKO}+\widehat{BKD}=\widehat{HAO}+\widehat{AHQ}=90^0\)
\(\Rightarrow\widehat{KIO}=90^0\)
\(\Rightarrow IK\)là tiếp tuyến của đường tròn \(\left(O\right)\)
(Hình vẽ chỉ mang tính chất minh họa cái hình vẽ gần cả tiếng đồng hồ :)) )

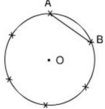
a) + Dùng compa vẽ đường tròn tâm O, bán kính R = 2cm.
+ Trên đường tròn lấy điểm A.Nối OA từ đó vẽ góc 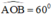
Khi đó ta được cung AB có số đo bằng 60 º .
+ ΔAOB có OA = OB,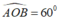
⇒ ΔAOB đều
⇒ AB = OA = OB = R = 2cm.
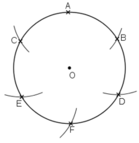
b) Chia đường tròn thành 6 cung bằng nhau:
+ Vẽ đường tròn tâm O, bán kính R.
+ Trên đường tròn tâm O, lấy điểm A.
+ Vẽ cung tròn tâm A, bán kính R cắt đường tròn tại B và C.
+ Vẽ cung tròn tâm B và C bán kính R cắt đường tròn tâm O tại giao điểm thứ hai là D và E.
+ Vẽ cung tròn tâm E bán kính R cắt đường tròn (O) tại giao điểm thứ hai là F.
Khi đó, ta chia được đường tròn thành sáu cung bằng nhau như trên