Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

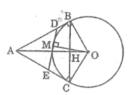
???ng tr�n c: ???ng tr�n qua B_1 v?i t�m O ?o?n th?ng h: ?o?n th?ng [A, B] ?o?n th?ng i: ?o?n th?ng [A, C] ?o?n th?ng k: ?o?n th?ng [D, E] ?o?n th?ng l: ?o?n th?ng [O, D] ?o?n th?ng m: ?o?n th?ng [O, E] ?o?n th?ng n: ?o?n th?ng [B, C] ?o?n th?ng p: ?o?n th?ng [B, O] ?o?n th?ng q: ?o?n th?ng [C, O] ?o?n th?ng r: ?o?n th?ng [D, K] ?o?n th?ng s: ?o?n th?ng [I, E] ?o?n th?ng t: ?o?n th?ng [O, M] O = (0.76, 0.64) O = (0.76, 0.64) O = (0.76, 0.64) ?i?m B: ?i?m tr�n c ?i?m B: ?i?m tr�n c ?i?m B: ?i?m tr�n c ?i?m C: ?i?m tr�n c ?i?m C: ?i?m tr�n c ?i?m C: ?i?m tr�n c ?i?m A: Giao ?i?m c?a f, g ?i?m A: Giao ?i?m c?a f, g ?i?m A: Giao ?i?m c?a f, g ?i?m M: ?i?m tr�n c ?i?m M: ?i?m tr�n c ?i?m M: ?i?m tr�n c ?i?m D: Giao ?i?m c?a j, h ?i?m D: Giao ?i?m c?a j, h ?i?m D: Giao ?i?m c?a j, h ?i?m E: Giao ?i?m c?a j, i ?i?m E: Giao ?i?m c?a j, i ?i?m E: Giao ?i?m c?a j, i ?i?m I: Giao ?i?m c?a l, n ?i?m I: Giao ?i?m c?a l, n ?i?m I: Giao ?i?m c?a l, n ?i?m K: Giao ?i?m c?a m, n ?i?m K: Giao ?i?m c?a m, n ?i?m K: Giao ?i?m c?a m, n
a. Ta thấy \(\widehat{CBA}=\frac{sđ\left(BC\right)}{2}\) (Kí hiệu số đo cùng BC là sđ(BC) )
Lại có \(\widehat{DOC}=\widehat{DOM}+\widehat{MOE}=\frac{\widehat{BOM}}{2}+\widehat{\frac{MOC}{2}}=\frac{\widehat{BOC}}{2}=\frac{sđ\left(BC\right)}{2}\)
Vậy \(\widehat{CBA}=\widehat{DOE}\)
Lại có \(\widehat{BDI}=\widehat{ODE}\) (Do BD và DM là hai tiếp tuyến)
Vậy nên \(\Delta BDI\sim\Delta ODE\left(g-g\right)\)
\(\Rightarrow\frac{DI}{DE}=\frac{BD}{OD}\Rightarrow DB.DE=DI.DO\left(đpcm\right)\)
b. Ta thấy do \(\Delta BDI\sim\Delta ODE\left(cmt\right)\Rightarrow\widehat{BID}=\widehat{OED}=\widehat{OEC}\)
\(\Rightarrow\)OIEC là tứ giác nội tiếp \(\Rightarrow\widehat{OIE}=\widehat{OCE}=90^o\Rightarrow EI\perp DO.\)
Tương tự \(DK\perp DE.\)
Xét tam giác ODE có OM, DK , EI là các đường cao nên chúng đồng quy.

chứng minh tứ giác OBDK nội tiếp:
dựa vào góc DBK=DOK (vì hai góc cùng chắn cung DK)
vậy, ta cần chứng minh DBK=DOK
đặt giao của OM với AB là H
dễ dàng chứng minh: DBK=BOA=1/2 BOC (1)
có M thuộc (O) và tiếp tuyến CD của M nên chứng minh được tam giác OBD=OMD (ch,cgv)
=> góc BOD=DOM và MOE=COE (chứng minh tương tự)
=> DOM+EOM=DOE=1/2BOM+1/2MOC=1/2BOC (2)
từ (1),(2) => DOK=KBD (đpcm)

Áp dụng định lí Pitago vào tam giác vuông ABO, ta có:
A O 2 = A B 2 + B O 2
Suy ra: A B 2 = A O 2 - B O 2 = 5 2 - 3 2 = 16
AB = 4 (cm)
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
DB = DM
EM = EC
Chu vi của tam giác ADE bằng:
AD + DE + EA = AD + DB + AE + EC
= AB + AC = 2AB = 2.4 = 8 (cm)