Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

d, Vi ED la tiep tuyen (chung minh tren) => tam giac EDF vuong tai D
co \(\widehat{CDE}=\frac{1}{2}sd\widebat{DC}=\frac{1}{2}\widehat{COD}=\frac{1}{2}.120=60^o\)
ma \(\widehat{CED}+\widehat{COD}=180^o\Rightarrow\widehat{CED}=180-120=60^o\)
suy ra \(\Delta CED\) deu => EC=CD (1)
mat khac cung co \(\widehat{CFD}=\widehat{CDF}\) (phu hai goc bang nhau)
=> tam giac CDF can tai C
suy ra CD=CF (2)
tu (1),(2) suy ra dpcm

a: Xét (O) có
OH là một phần đường kính
AB là dây
OH⊥AB tại H
Do đó: H là trung điểm của AB
Xét ΔMAB có
MH là đường trung tuyến
MH là đường cao
Do đó:ΔMAB cân tại M
Xét ΔOAM và ΔOBM có
OA=OB
AM=BM
OM chung
Do đó:ΔOAM=ΔOBM
Suy ra: \(\widehat{OAM}=\widehat{OBM}=90^0\)
=>ΔOMB vuông tại B
=>MB là tiếp tuyến
b: Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó:ΔABC vuông tại A

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)

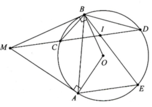
a, Vì M B C ^ = M D B ^ = 1 2 s đ C B ⏜ nên chứng minh được ∆MBC:∆MDB (g.g)
b, Vì
M
B
O
^
+
M
A
O
^
=
180
0
nên tứ giác MAOB nội tiếp
c, Đường tròn đường kính OM là đường tròn ngoại tiếp tứ giác MAOB => r = M O 2
Gọi H là giao điểm của AB với OM
=> OH ⊥ AB; AH = BH = R 3 2
Giải tam giác vuông OAM, đường cao AH ta được OM = 2R Þ r = R
d, Ta có M I B ^ = s đ D E ⏜ + s đ B C ⏜ 2 và M A B ^ = s đ A C ⏜ + s đ B C ⏜ 2
Vì AE song song CD => s đ D E ⏜ = s đ A C ⏜ => M I B ^ = M A B ^
Do tứ giác MAIB nội tiếp hay 5 điểm A, B, O, I, M nằm trên cùng 1 đường tròn kính MO
Từ đó ta có được M I O ^ = 90 0 => OI ⊥ CD hay I là trung điểm của CD
A B C D Q M O
a/ Xét \(\Delta OAC\) có
OA=OC=AC=R =>\(\Delta OAC\) là tg đều
b/ Gọi I là giao của CD với AB
\(AB\perp CD\Rightarrow IC=ID\) (trong đường tròn đường kính vuông góc với dây cung thì chia đôi dây cung) (1)
\(CD\perp AB\) => CD là đường cao của tg OAC => CD là trung tuyến của tg OAC (trong tg cân đường cao xp từ đỉnh đồng thời là đường trung tuyến) => IA=IO (2)
Từ (1) và (2) => ACOD là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
\(CD\perp AB\Rightarrow CD\perp AO\)
=> ACOD là hình thoi (Hình bình hành có hai đường chéo vuông góc là hình thoi)
c/
Ta có
\(IA=IO\Rightarrow IO=\frac{OA}{2}=\frac{R}{2}\)
Xét tg vuông COI có \(IC=\sqrt{OC^2-IO^2}=\sqrt{R^2-\frac{R^2}{4}}=\frac{R\sqrt{3}}{2}\)
\(BI=OB+IO=R+\frac{R}{2}=\frac{3R}{2}\)
Xét tg vuông IBC có \(BC=\sqrt{BI^2+IC^2}=\sqrt{\frac{9R^2}{4}+\frac{3R^2}{4}}=R\sqrt{3}\)
d/
Ta có \(\widehat{ACB}=90^o\)(góc nội tiếp chắn nửa đường tròn) \(\Rightarrow\widehat{BCQ}=90^o\)
=> C nhìn BQ dưới 1 góc vuông => C thuộc đường tròn đường kính BQ. Đây chính là đường tròn ngoại tiếp tg BCQ
Ta có \(\widehat{BCO}=\widehat{BCA}-\widehat{ACO}=90^o-60^o=30^o\)
\(sd\widehat{CAB}=\frac{1}{2}sd\) cung BC (góc nội tiếp đường tròn) (1)
\(sd\widehat{CBM}=\frac{1}{2}sd\)cung BC (góc giữa tiếp tuyến và dây cung) (2)
Gọi M là tâm đường tròn ngoại tiếp tg BCQ => MQ=MB
Ta có MC = MQ = MB (trong tg vuông trung tuyến thuộc cạnh huyền thì bằng nửa cạnh huyền)
=> tg MBC cân tại M \(\Rightarrow\widehat{BCM}=\widehat{CBM}\) (góc ở đáy tg cân) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{BCM}=\widehat{CAB}=60^o\)
\(\Rightarrow\widehat{OCM}=\widehat{BCM}+\widehat{BCO}=60^o+30^o=90^o\Rightarrow OC\perp MC\)=> OC là tiếp tuyến của đường tròn ngoại tiếp tg BCQ