Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(l = R\alpha = 20.\frac{\pi }{{12}} = \frac{{5\pi }}{3}\)
b) \(l = R\alpha = 20.1,5\pi = 30\pi \)
c) Đổi \({35^0} = 35.\frac{\pi }{{180}} = \frac{7\pi }{36}\)
\(l = R\alpha = 20.\frac{7\pi }{36} = \frac{35\pi }{9}\)
d) Đổi \({315^0} = 315.\frac{\pi }{{180}} = \frac{{7\pi }}{4}\)
\(l = R\alpha = 20.\left( {\frac{{7\pi }}{4}} \right) = 35\pi \)

Ta có: \(\alpha=\left(\dfrac{1}{60}\right)^o\Rightarrow\alpha=\dfrac{\left(\pi\cdot\dfrac{1}{60}\right)}{180}=\dfrac{\pi}{10800}\)
Vậy một hải lí có độ dài bằng:
\(l=\dfrac{\pi Rn^o}{180^o}=\dfrac{\pi\cdot6371\cdot\left(\dfrac{1}{60}\right)^o}{180^o}\approx1,85\left(km\right)\)

Ta có tam giác OBC đều, đường cao OI = (R√3)/2
⇒ I chạy trên đường tròn tâm O bán kính (R√3)/2.
Vì A cố định, G là trọng tâm tam giác ABC nên A G → = 2 3 A I →
⇒ có phép vị tự tâm A tỉ số k = 2/3 biến đường tròn (O;(R√3)/2) thành đường tròn (O';R’) với R ' = R 3 2 . 2 3 = R 3 3
Chọn đáp án C
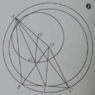

1. Cho đường tròn (O;R) và 1 điểm A cố định trên đường tròn, BC là 1 dây cung di động của đường tròn này và BC có độ dài không đổi = 2d (d<R). Tìm tập hợp trọng tâm G của ΔABC

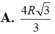
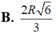
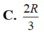
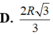
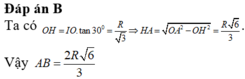
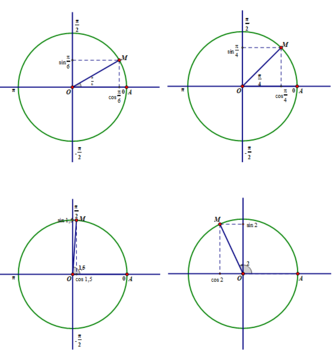
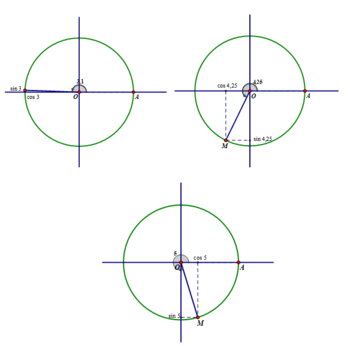
a) Độ dài của cung tròn có số đo bằng 1 rad là bằng bán kính R.
b) Độ dài l của cung tròn có số đo \(\alpha \) rad: \(l = R\alpha \).