Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: A(1;2); B(2;1)
=>\(\overrightarrow{AB}=\left(1;-1\right)\)
=>VTPT là (1;1)
Phương trình đường thẳng AB là:
1(x-1)+2(y-1)=0
=>x-1+2y-2=0
=>x+2y-3=0
b:
M(1;3); Δ: 3x+4y+10=0
Khoảng cách từ M đến Δ là:
\(d\left(M;\text{Δ}\right)=\dfrac{\left|1\cdot3+3\cdot4+10\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|3+12+10\right|}{5}=5\)

Lấy điểm M( x0; 1-2x0) nằm trên d.
Từ giả thiết ta có:
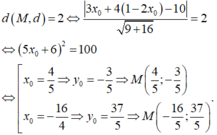
Chọn C.

Đáp án: D
Khoảng cách từ điểm M(3;-4) đến đường thẳng d: 3x - 4y - 1 = 0 là:
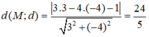

Áp dụng công thức tính khoảng cách từ 1 điểm đến 1 đường thẳng ta có:
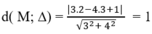
Chọn A.

\(d\left(M;\Delta\right)=\dfrac{\left|3.2+4.5-m\right|}{\sqrt{3^2+4^2}}=1\)
\(\Leftrightarrow\left|26-m\right|=5\Rightarrow\left[{}\begin{matrix}m=21\\m=31\end{matrix}\right.\)
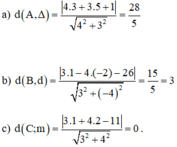

Lời giải:
Khoảng cách từ điểm $N$ đến $d$ bạn chỉ cần áp dụng công thức thôi:
\(d(N,d)=\frac{|3.2+4(-1)-10|}{\sqrt{3^2+4^2}}=\frac{8}{5}\)
Ghi nhớ: Đường thẳng \( ax+by+c=0\) thì khoảng cách từ \(M(x_0;y_0)\) đến đường thẳng đã cho là:
\(d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\)