Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vẽ tia CO cắt tia đối của tia By tại E
Xét tam giác vuông AOC và tam giác vuông BOE có :
AO = OB ( gt )
AOC = BOE ( 2 góc đối đỉnh )
\(\implies\) tam giác vuông AOC = tam giác vuông BOE ( cạnh huyền - góc nhọn )
\(\implies\) AC = BE ( 2 cạnh tương ứng )
Xét tam giác vuông DOC và tam giác vuông DOE có :
OD chung
OC = OE ( tam giác vuông AOC = tam giác vuông BOE )
\(\implies\) tam giác vuông DOC = tam giác vuông DOE ( 2 cạnh góc vuông )
\(\implies\) CD = ED ( 2 cạnh tương ứng )
Mà ED = EB + BD
\(\implies\) ED = AC + BD
\(\implies\) CD = AC + BD
c) Xét tam giác DOE vuông tại O có :
OE2 + OD2 = DE2 ( Theo định lý Py - ta - go )
Xét tam giác BOE vuông tại B có :
OB2 + BE2 = OE2 ( Theo định lý Py - ta - go ) ( * )
Xét tam giác BOD vuông tại B có :
OB2 + BD2 = OD2 ( Theo định lý Py - ta - go ) ( ** )
Cộng ( * ) với ( ** ) vế với vế ta được :
OE2 + OD2 = 2. OB2 + EB2 + DB2
Mà OE2 + OD2 = DE2 ( cmt )
\(\implies\) DE2 = 2. OB2 + EB2 + DB2
= 2. OB2 + EB . ( DE - BD ) + DB . ( DE - BE )
= 2. OB2 + EB . DE - EB . BD + DB . DE - DB . BE
= 2. OB2 + ( EB . DE + DB . DE ) - 2 . BD . BE
= 2. OB2 + DE . ( EB + DB ) - 2 . BD . BE
= 2. OB2 + DE2 - 2 . BD . BE
\(\implies\) 2. OB2 - 2 . BD . BE = 0
\(\implies\) 2. OB2 = 2 . BD . BE
\(\implies\) OB2 = BD . BE
Mà BE = AC ( cmt ) ; OB = AB / 2 ( gt )
\(\implies\) AC . BD = ( AB / 2 )2
\(\implies\) AC . BD = AB2 / 4

a, Xét tam giác DOB và tam giác IOA ta có :
^DOB = ^IOA ( đối đỉnh )
^AIO = ^ODB ( DB // CA do cùng vuông AB và 2 góc này ở vị trí so le trong )
^OAI = ^OBD = 900
Vậy tam giác DOB = tam giác IOA ( ch - gn )
=> OD = OI ( 2 góc tương ứng )
b, Xét tam giác ICD có CO vuông ID hay CO là đường cao
Lại có IO = OD ( cmt ) => CO là đường trung tuyến
=> tam giác ICD cân tại C => CI = CD (2)
Mặt khác : tam giác DOB = tam giác IOA ( cmt ) => BD = IA (1)
=> CI = AC + IA lại có (1) ; (2) => CD = AC + BD
c, Dựng OH vuông CD
Xét tam giác DHO và tam giác HBO ta có :
^DHO = ^HBO = 900
^HDO = ^ODB ( cùng ''='' ^CID )
OD _ chung
Vậy tam giác DHO = tam giác HBO ( g.c.g )
=> OH = OB = R
Vậy CD là tiếp tuyến đường tròn (O)

a ) ta có OD là phân giác góc MOA ( tính chất 2 tiếp tuyến cắt nhau )
vầ OC là phân giác góc MOB ( tính chất 2 tiếp tuyết cắt nhau )
Mà góc MOA + MOD =180 độ
từ 3 cái đó suy ra Góc COD vuông hay tam giác COD =90 độ
b ) ta có AD=DM ( tính chất 2 tiếp tuyến cắt nhau ) (1)
và MC=BC( tính chất 2 tiếp tuyến cắt nhau ) (2)
mặt khác ta có DM+MC =DC
Từ 1 và 2 suy ra : AD+BC =CD
theo cách mình nghĩ là nhưng thế , nhưng phần c mình đang nghĩ hihi

a: Kẻ CO cắt BD tại E
Xét ΔOAC vuông tại A và ΔOBE vuông tại B có
OA=OB
góc COA=góc EOB
Do đó: ΔOAC=ΔOBE
=>OC=OE
Xét ΔDCE có
DO vừa là đường cao, vừalà trung tuyến
nên ΔDEC cân tại D
=>góc DCE=góc DEC=góc CAO
=>CO là phân giác của góc DCA
Kẻ CH vuông góc với CD
Xét ΔCAO vuông tại A và ΔCHO vuông tại H có
CO chung
góc ACO=góc HCO
DO đó: ΔCAO=ΔCHO
=>OA=OH=OB và CH=CA
Xét ΔOHD vuông tại H và ΔOBD vuông tại B có
OD chung
OH=OB
Do đó: ΔOHD=ΔOBD
=>DH=DB
=>AC+BD=CD
b: Gọi M là trung điểm của CD
Xét hình thang ABDC có
O,M lần lượt là trung điểm của AB,CD
nên OM la đường trung bình
=>OM//AC//BD
=>OM vuông góc với AB
=>CD là tiếp tuyến của (O)
c: AC*BD=CH*HD=OH^2=R^2=AB^2/4

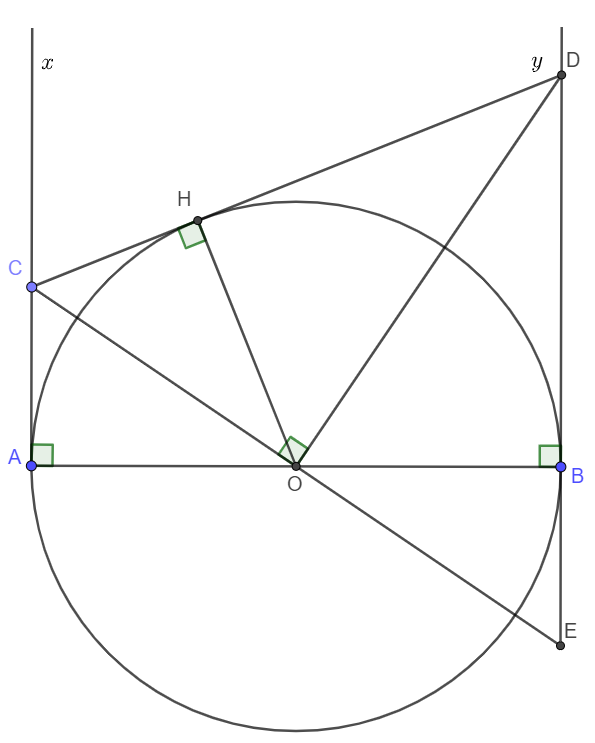
Vẽ OH\perp CD\left(H\in CD\right)OH⊥CD(H∈CD). Ta chứng minh OH = r = OB. (r là bán kính của đường tròn (O) ).
Tia CO cắt tia đối của tia By tại E.
Ta có \Delta OAC=\Delta OBE\left(g.c.g\right)\Rightarrow OC=OEΔOAC=ΔOBE(g.c.g)⇒OC=OE.
Tam giác DEC có DO vừa là đường cao vừa là đường trung tuyến nên DEC là tam giác cân tại D.
Khi đó DO cũng là đường phân giác.
OH\perp DC,OB\perp DE\Rightarrow OH=OB.OH⊥DC,OB⊥DE⇒OH=OB..
Suy ra CD tiếp xúc với (O) tại H.
Ta có OH\perp CD,OH=OB=rOH⊥CD,OH=OB=r.
Vậy CD là tiếp tuyến của đường tròn (O).
Vẽ OH⊥CD(H∈CD). Ta chứng minh OH = r = OB. (r là bán kính của đường tròn (O) ).
Tia CO cắt tia đối của tia By tại E.
Ta có ΔOAC=ΔOBE(g.c.g)⇒OC=OE.
Tam giác DEC có DO vừa là đường cao vừa là đường trung tuyến nên DEC là tam giác cân tại D.
Khi đó DO cũng là đường phân giác.
OH⊥DC,OB⊥DE⇒OH=OB..
Suy ra CD tiếp xúc với (O) tại H.
Ta có OH⊥CD,OH=OB=r.
Vậy CD là tiếp tuyến của đường tròn (O).