Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A P R C H E M F B Q N L S K D I
a) Kẻ CE, IH, DF vuông góc với AB.
Ta chứng minh được
CE = \(\dfrac{AM}{2},\) DF = \(\dfrac{MB}{2},\)
CE + DF = \(\dfrac{AB}{2}=\dfrac{a}{2}\)
nên IH = \(\dfrac{a}{4}.\)
b) Khi điểm M di chuyển trên đoạn thẳng AB thì I di chuyển trên đoạn thẳng RS song song với AB và cách AB một khoảng bằng \(\dfrac{a}{4}\) (R là trung điểm của AQ, S là trung điểm của BQ, Q là giao điểm của BL và AN).

H�nh ?a gi�c TenDaGiac1: DaGiac[A, M, 4] H�nh ?a gi�c TenDaGiac2: DaGiac[M, B, 4] ?o?n th?ng f: ?o?n th?ng [A, B] ?o?n th?ng g: ?o?n th?ng [A, M] c?a H�nh ?a gi�c TenDaGiac1 ?o?n th?ng h: ?o?n th?ng [M, N] c?a H�nh ?a gi�c TenDaGiac1 ?o?n th?ng i: ?o?n th?ng [N, P] c?a H�nh ?a gi�c TenDaGiac1 ?o?n th?ng j: ?o?n th?ng [P, A] c?a H�nh ?a gi�c TenDaGiac1 ?o?n th?ng k: ?o?n th?ng [M, B] c?a H�nh ?a gi�c TenDaGiac2 ?o?n th?ng l: ?o?n th?ng [B, K] c?a H�nh ?a gi�c TenDaGiac2 ?o?n th?ng m: ?o?n th?ng [K, L] c?a H�nh ?a gi�c TenDaGiac2 ?o?n th?ng L_1: ?o?n th?ng [L, M] c?a H�nh ?a gi�c TenDaGiac2 ?o?n th?ng s: ?o?n th?ng [C, D] ?o?n th?ng d: ?o?n th?ng [I, J] ?o?n th?ng e: ?o?n th?ng [C, E] ?o?n th?ng f_1: ?o?n th?ng [D, G] A = (-1.16, 1) A = (-1.16, 1) A = (-1.16, 1) B = (6.34, 1.14) B = (6.34, 1.14) B = (6.34, 1.14) ?i?m M: ?i?m tr�n f ?i?m M: ?i?m tr�n f ?i?m M: ?i?m tr�n f ?i?m N: DaGiac[A, M, 4] ?i?m N: DaGiac[A, M, 4] ?i?m N: DaGiac[A, M, 4] ?i?m P: DaGiac[A, M, 4] ?i?m P: DaGiac[A, M, 4] ?i?m P: DaGiac[A, M, 4] ?i?m K: DaGiac[M, B, 4] ?i?m K: DaGiac[M, B, 4] ?i?m K: DaGiac[M, B, 4] ?i?m L: DaGiac[M, B, 4] ?i?m L: DaGiac[M, B, 4] ?i?m L: DaGiac[M, B, 4] ?i?m C: Giao ?i?m c?a n, p ?i?m C: Giao ?i?m c?a n, p ?i?m C: Giao ?i?m c?a n, p ?i?m D: Giao ?i?m c?a q, r ?i?m D: Giao ?i?m c?a q, r ?i?m D: Giao ?i?m c?a q, r ?i?m I: Trung ?i?m c?a C, D ?i?m I: Trung ?i?m c?a C, D ?i?m I: Trung ?i?m c?a C, D ?i?m E: Giao ?i?m c?a t, f ?i?m E: Giao ?i?m c?a t, f ?i?m E: Giao ?i?m c?a t, f ?i?m G: Giao ?i?m c?a a, f ?i?m G: Giao ?i?m c?a a, f ?i?m G: Giao ?i?m c?a a, f ?i?m J: ?i?m tr�n f ?i?m J: ?i?m tr�n f ?i?m J: ?i?m tr�n f
a. Kẻ \(CE\perp AM;DG\perp MB\) , ta thấy ngay CE = EM; DG = GM (Do AMNP, BMLKA là hình vuông)
Từ I kẻ IJ // CE // DG : IJ là đường trung bình hình thang CEGD. Vậy thì
\(IJ=\frac{EC+DG}{2}=\frac{EM+MG}{2}=\frac{AB}{4}=\frac{a}{4}.\)
Do \(IJ\perp AB\) nên khoảng cách từ I tới AB là IJ = \(\frac{a}{4}.\)
b. Do khoảng cách từ I tới AB không thay đổi nên khi M di chuyển trên AB thì I di chuyển trên đường thẳng song song AB, cách AB một khoảng bằng \(\frac{a}{4}.\)
Bài của mình giống cô giáo :
Câu hỏi của Nguyễn Minh Phương - Toán lớp 8 - Học toán với OnlineMath
Cậu tahm khảo bài của cô nha

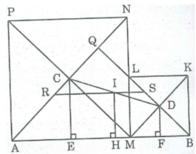
Gọi Q là giao điểm của BL và AN.
Ta có:
AN ⊥ MP (tính chất hình vuông)
BL ⊥ MK (tính chất hình vuông)
MP ⊥ MK (tính chất hình vuông)
Suy ra:
BL ⊥ AN ⇒ ∆ QAB vuông cân tại Q cố định.
M thayđổi thì I thay đổi luôn cách đoạn thẳng AB cố định một khoảng không đổi bằng a/4 nên I chuyển động trênđường thẳng song song với AB, cách AB một khoảng bằng a/4.
Khi M trùng B thì I trùng với S là trung điểm của BQ.
Khi M trùng với A thì I trùng với R là trung điểm của AQ.
Vậy khi M chuyển động trên đoạn AB thì I chuyển động trên đoạn thẳng RS song song với AB, cách AB một khoảng bằng a/4

https://olm.vn/hoi-dap/detail/61999750098.html
Câu hỏi của Hoàng Phúc - Toán lớp 8 - Học toán với OnlineMath
Một cách của a@olm.vn
cần gấp ae ơi