Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

D là TĐ của AB mà DE //BC nên DE là đg TB của tam giác ABC -->E là TĐ của AC.
E là TĐ của AC mà EF //AB nên EF là đg TB của tam giác CAB--->F là TĐ của BC

a: Xét tứ giác BDEF có
DE//BF
BD//EF
Do đó: BDEF là hình bình hành
Suy ra: EF=BD
mà BD=AD
nên EF=AD
b: Xét ΔADF và ΔFEA có
AD=FE
AF chung
DF=EA
Do đó: ΔADF=ΔFEA

NGU NHƯ BÒÔFÔFÒÔFÔFÔFFÒÔFFÔFOFOFÔFỒ
RỨA MÀ KHÔNG LÀM ĐƯỢC NGU VL NGU VCL NGU VÃI LINH HỒN NGU VÃI L*N CHIM ÉN
xet tam giac BDF va tam giac DEF ta co
DF=DF ( canh chung)
goc BDF = goc DFE ( 2 goc sole trong va BA//EF)xet tam giac BDF va tam giac DEF ta co
DF=DF ( canh chung)
goc BDF = goc DFE ( 2 goc sole trong va BA//EF)
goc DFB = goc FDE ( 2 goc sole trong va DE//BC)
--> tam giac BDF = tam giac DEF ( g-c-g)
--> BD= EF ( 2 goc tuong ung)
ma AD=BD ( D la trung diem AB)
nen AD=EF
b)ta co
goc ADE=goc BAC ( 2 goc dong vi va DE//BC)
goc CEF = goc BAC ( 2 goc dong vu va EF//AB)
--> goc ADE = goc CFE
xet tam giac ADE va tam giac EFC ta co
goc ADE=goc CFE ( cmt
AD= EF ( cm a)
goc DAE = goc FEC ( 2 goc dong vi va DE//BC)
--> tam giac ADE = tam giac EFC ( c-g-c)
c) tam giac ADE= tam giac EFC (cmt)--> AE=EC
goc DFB = goc FDE ( 2 goc sole trong va DE//BC)
--> tam giac BDF = tam giac DEF ( g-c-g)
--> BD= EF ( 2 goc tuong ung)
ma AD=BD ( D la trung diem AB)
nen AD=EF
b)ta co
goc ADE=goc BAC ( 2 goc dong vi va DE//BC)
goc CEF = goc BAC ( 2 goc dong vu va EF//AB)
--> goc ADE = goc CFE
xet tam giac ADE va tam giac EFC ta co
goc ADE=goc CFE ( cmt
AD= EF ( cm a)
goc DAE = goc FEC ( 2 goc dong vi va DE//BC)
--> tam giac ADE = tam giac EFC ( c-g-c)
c) tam giac ADE= tam giac EFC (cmt)--> AE=EC

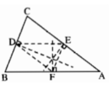
+)Xét tam giác BDF và ∆EFD có:
DF chung
∠BDF = ∠DFE ( hai góc so le trong; BC// EF)
∠BFD = ∠FDE ( hai góc so le trong; DE// AB)
Suy ra:∆ BDF = ∆EFD (g.c.g)
Suy ra BD = EF. Theo giả thiết, D là trung điểm của BC nên CD = DB = EF.
+) Xét ∆ CDE và ∆ EFA có :
CD = EF ( chứng minh trên)
∠(CDE) = ∠(EFA) = ∠(CBA)
∠(ECD) = ∠(AEF) (các góc đồng vị).
Suy ra: ∆ CDE = ∆ EFA ( g.c.g)
Suy ra CE = EA nên E là trung điểm của CD.

A B C E F D
a) Co E la trung diem cua AC, FE//BC suy ra F la trung diem AB(duong trung binh )
Co E la trung diem AC, ED//AB suy ra D la trung diem BC(duong trung binh)
b) Co F la trung diem AB (cmt), D la trung diem BC (cmt) suy ra FD la duong trung binh cua tam giac ABC
suy ra FD//=1/2 AC (t/c duong trung binh)
A C B D E F
a) Xét △AFD và △EDF có:
∠AFD = ∠EDF (so le trong)
FD chung
∠FDA = ∠DFE (so le trong)
⇒△AFD=△EDF (gcg)
⇒AD=EF (2 cạnh tương ứng) mà AD=CD⇒EF=CD
Ta có:
∠CDE=∠DEF( so le trong)
∠DEF=∠BFE( so le trong)
⇒∠CDE=∠BFE
Xét △BEF và △ECD có:
∠BFE=∠EDC (cmt)
FE=DC (cmt)
∠FEB=∠DCE (đồng vị)
⇒△BEF =△ECD (gcg)
b) △BEF =△ECD (câu a)
⇒BF=ED (2 cạnh tương ứng) mà △AFD=△EDF (câu a)⇒AF=ED (2 cạnh tương ứng)
⇒BF=AF⇒ F là trung điểm của AB (Chỗ này đề sai bạn nhé!)
△BEF =△ECD (câu a)
⇒BE=EC (2 cạnh tương ứng)
⇒E là trung điểm của BC