Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo bạn thì câu trả lời sẽ là bao nhiêu? Cách giải thứ nhất là cộng kết quả hàng trên với số đầu hàng dưới lại, chúng ta sẽ có kết quả hàng dưới (1 + 4 = 5, 5 + 2 + 5 = 12,...), cứ thế, ta sẽ có con số cuối cùng là 40.
Tuy nhiên vẫn còn một cách giải khác, đó là nhân số thứ hai trong phép tính với số đầu rồi tiếp tục cộng thêm số đầu (4 x 1 + 1 = 5, 5 x 2 + 2 = 12...), nếu tính theo cách này thì đáp án cuối sẽ là 96.
làm bừa thui,ai trên 11 điểm tích mình mình tích lại
Số số hạng là :
Có số cặp là :
50 : 2 = 25 ( cặp )
Mỗi cặp có giá trị là :
99 - 97 = 2
Tổng dãy trên là :
25 x 2 = 50
Đáp số : 50

a: Đặt BH=x; CH=y
ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC
=>x*y=144
mà x+y=25
nên x,y là các nghiệm của phương trình:
a^2-25a+144=0
=>a=9 hoặc a=16
=>BH=9cm; CH=16cm
\(AB=\sqrt{9\cdot25}=15\left(cm\right)\)
\(AC=\sqrt{16\cdot25}=20\left(cm\right)\)
\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
b: ΔABC vuông tại A có AM là trung tuyến
nên AM=BC/2=12,5cm
Xét ΔAHM vuông tại H có sin AMH=AH/AM=24/25
nên \(\widehat{AMH}\simeq74^0\)
c: HM=căn AM^2-AH^2=3,5cm
S AHM=1/2*HM*AH=1/2*12*3,5=21cm2

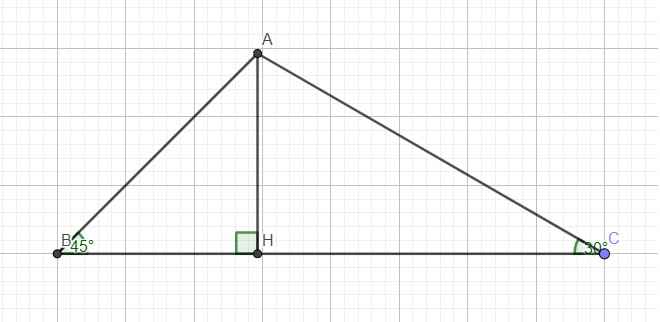
a.
Trong tam giác vuông ABH ta có:
\(cotB=\dfrac{BH}{AH}\Rightarrow BH=AH.cotB\)
Trong tam giác vuông ACH ta có:
\(cotC=\dfrac{CH}{AH}\Rightarrow CH=AH.cotC\)
\(\Rightarrow BH+CH=AH.cotB+AH.cotC\)
\(\Leftrightarrow BC=AH\left(cotB+cotC\right)\)
\(\Leftrightarrow AH=\dfrac{BC}{cotB+cotC}\) (đpcm)
b. Áp dụng công thức câu a:
\(AH=\dfrac{4}{cot45^0+cot30^0}=-2+2\sqrt{3}\) (cm)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\left(-2+2\sqrt{3}\right).4=-4+4\sqrt{3}\approx2,93\left(cm^2\right)\)

Kẻ đg cao AH, trung tuyến AD, trọng tâm G
Tg AHD vuông tại H nên \(AH\le AD\Rightarrow\dfrac{BC}{AH}\ge\dfrac{BC}{AD}\left(4\right)\)
Ta có \(\cot\widehat{B}+\cot\widehat{C}=\dfrac{BH}{AH}+\dfrac{CH}{AH}=\dfrac{BC}{AH}\ge\dfrac{BC}{AD}\left(1\right)\)
Mà BM vuông góc CN nên GD là trung tuyến ứng vs ch BC
\(\Rightarrow BC=2GD\left(2\right)\)
Mà G là trọng tâm nên \(3GD=AD\left(3\right)\)
\(\left(1\right)\left(2\right)\left(3\right)\left(4\right)\Rightarrow\cot\widehat{B}+\cot\widehat{C}\ge\dfrac{BC}{AD}=\dfrac{2GD}{3GD}=\dfrac{2}{3}\)