Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(E = \{ x \in \mathbb{N}|x < 8\} = \{ 0;1;2;3;4;5;6;7\} \)
a) Ta có: \(A\backslash B = \left\{ {0;1;2} \right\}\), \(B\backslash A = \left\{ 5 \right\},\)\((A\backslash B) \cap {\rm{(}}B\backslash A) = \emptyset \)
b) Ta có: \(A \cap B = \{ 3;4\} ,\;{C_E}(A \cap B) = \{ 0;1;2;5;6;7\} \)
\({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\} \Rightarrow ({C_E}A) \cap ({C_E}B) = \{ 6;7\} \)
c) Ta có: \(A \cup B = \{ 0;1;2;3;4;5\} ,\;{C_E}(A \cup B) = \{ 6;7\} \)
\({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\} \Rightarrow ({C_E}A) \cup ({C_E}B) = \{ 0;1;2;5;6;7\} \)

a, \(A\cup B=(-4;5]\)
\(A\cap B=[-3;4)\)
\(A\backslash B=\left[4;5\right]\)
\(B\backslash A=\left(-4;-3\right)\)
b, \(A\cup B=\left(-3;7\right)\)
\(A\cap B=[1;2)\cup(3;5]\)
\(A\backslash B=\left[2;3\right]\)
\(B\backslash A=\left(-3;1\right)\cup\left(5;7\right)\)
c, \(A\cup B=\left[\dfrac{1}{2};3\right]\)
\(A\cap B=\left[1;\dfrac{3}{2}\right]\)
\(A\backslash B=[\dfrac{1}{2};1)\)
\(B\backslash A=(\dfrac{3}{2};3]\)
d, \(A\cup B=(-5;2]\cup(3;6]\)
\(A\cap B=\left\{0\right\}\cup[4;5)\)
\(A\backslash B=(0;2]\cup\left[-5;6\right]\)
\(B\backslash A=[-5;0)\cup\left(3;4\right)\)

\(E = \{ x \in \mathbb{N}|x < 10\} = \{ 0;1;2;3;4;5;6;7;8;9\} \)
\(A = \{ x \in E|x\) là bội của 3\(\} \)\( = \{ 0;3;6;9\} \)
\(B = \{ x \in E|x\) là ước của 6\(\} \)\( = \{1;2;3;6\} \)
Ta có: \(A\backslash B = \left\{ {0;9} \right\}\), \(B\backslash A = \left\{ {1;2} \right\}\)
\({C_E}A = \{ 1;2;4;5;7;8\} ,\;{C_E}B = \{ 0;4;5;7;8;9\} \)
\(A \cap B = \{ 3;6\} \Rightarrow {C_E}(A \cap B) = {C_E}B = \{0;1;2;4;5;7;8;9\} \)
\(A \cup B = \{ 0;1;2;3;6;9\} \Rightarrow {C_E}(A \cup B) = {C_E}A = \{ 4;5;7;8\} \)

Tham khảo:
+) \(A \cap B = [0;3] \cap (2; + \infty ) = (2;3]\)

+) \(A \cup B = [0;3] \cup (2; + \infty ) = [0; + \infty )\)

+) \(A\,{\rm{\backslash }}\,B = [0;3]\,{\rm{\backslash }}\,(2; + \infty ) = [0;2]\)

+) \(B\,{\rm{\backslash }}\,A = (2; + \infty )\,{\rm{\backslash }}\,[0;3] = (3; + \infty )\)

+) \(\mathbb{R}\,{\rm{\backslash }}\,B = \mathbb{R}\,{\rm{\backslash }}\,(2; + \infty ) = ( - \infty ;2]\)


Ta có: \(A = \left\{ {x \in \mathbb{Z}| - 2 \le x \le 3} \right\} = \{ - 2; - 1;0;1;2;3\} \)
Và \(B = \{ x \in \mathbb{R}|{x^2} - x - 6 = 0\} = \{ - 2;3\} \)
Khi đó:
Tập hợp \(A\,{\rm{\backslash }}\,B\) gồm các phần tử thuộc A mà không thuộc B. Vậy\(A\,{\rm{\backslash }}\,B = \{ - 1;0;1;2\} \).
Tập hợp \(B\,{\rm{\backslash }}\,A\) gồm các phần tử thuộc B mà không thuộc A. Vậy \(B\,{\rm{\backslash }}\,A = \emptyset \)

a) Liệt kê các phần tử của tập hợp �={�∈�∣ 2�2+3�+1=0 }A={x∈Z 2x2+3x+1=0 }
Ta có: 2�2+3�+1=0⇔[ �=−12 �=−1 2x2+3x+1=0⇔ x=−21 x=−1 .
Do đó: �={−1}A={−1}.
b) Cho hai tập hợp �={�∈�∣∣�∣>4}A={x∈R∣x∣>4} và �={�∈�∣−5≤�−1<5}B={x∈R−5≤x−1<5}. Xác định tập �=�\�X=B\A.
Ta có:
⚡∣�∣>4⇔[ �>4 �<−4⇒�=(−∞;−4)∪(4;+∞ )∣x∣>4⇔[ x>4x<−4⇒A=(−∞;−4)∪(4;+∞ ).
⚡−5≤�−1<5⇔−4≤�<6⇒�=[−4;6)−5≤x−1<5⇔−4≤x<6⇒B=[−4;6).
Suy ra �=�\�=[−4;4]X=B\A=[−4;4].

\(C\cap B=[-5;a]\)
mà \(B=\left\{x\in R|-5\le x\le5\right\}\) có độ dài là \(\left|-5\right|+\left|5\right|=10\)
\(\Rightarrow C\cap B=[-5;a]\) có độ dài là \(5\) thì \(a=10:2-5=0\)
\(D\cap B=[b;5]\) có độ dài là 9 thì \(b=10:2-9=-4\)

Phương trình \({x^2} - 5x - 6 = 0\) có hai nghiệm là -1 và 6, nên \(A = \{ - 1;6\} \)
Phương trình \({x^2} = 1\) có hai nghiệm là 1 và -1, nên \(B = \{ - 1;1\} \)
Do đó
\(\begin{array}{l}A \cap B = \{ - 1\} ,\\A \cup B = \{ - 1;1;6\} ,\\A\backslash B = \{ 6\} ,\\B\backslash A = \{ 1\} ,\end{array}\)
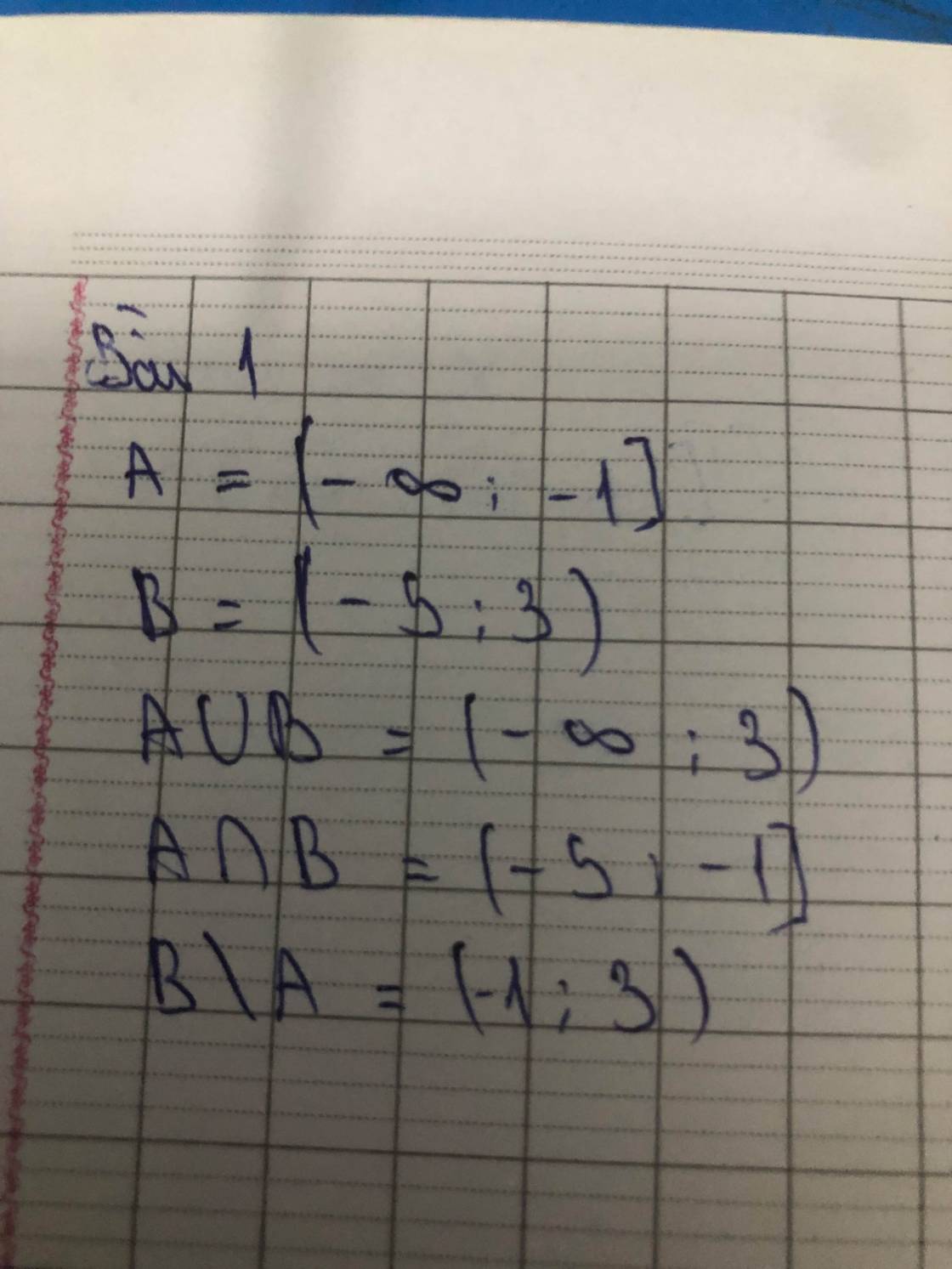
\(A = \left\{ {0;1;2;3;4;5;6} \right\}\)
\(\,B = \left\{ {1;2;3;6;7;8} \right\}\)
Vậy
\(A \cap B = \left\{ {1;2;3;6} \right\}\)
\(A \cup B = \left\{ {0;1;2;3;4;5;6;7;8} \right\} = \left\{ {x \in \mathbb{N}|\;x < 9} \right\}\)
\(A\;{\rm{\backslash }}\;B = \left\{ {0;4;5} \right\}\)