Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{8a^2+b}{4a}+b^2=2a+\frac{b}{4a}+b^2=a+a+\frac{b}{4a}+b^2\)
\(\ge a+1-b+\frac{1-a}{4a}+b^2=a+1-b+\frac{1}{4a}-\frac{1}{4}+b^2\)(do \(a+b\ge1\))
\(=\left(a+\frac{1}{4a}\right)+b^2-b+\frac{1}{4}+\frac{1}{2}\)
\(\ge2\sqrt{a\cdot\frac{1}{4a}}+\left(b-\frac{1}{2}\right)^2+\frac{1}{2}\)
\(\ge2\cdot\frac{1}{2}+\frac{1}{2}=\frac{3}{2}\)
Dấu = khi \(a=b=\frac{1}{2}\)

\(A=2a+\frac{b}{4a}+b^2=a+a+\frac{b}{4a}+b^2\)
\(A\ge a+1-b+\frac{1-a}{4a}+b^2\)
\(A\ge a+\frac{1}{4a}+b^2-b=a+\frac{1}{4a}+\left(b-\frac{1}{2}\right)^2-\frac{1}{4}\)
\(A\ge a+\frac{1}{4a}-\frac{1}{4}\ge2\sqrt{\frac{a}{4a}}-\frac{1}{4}=\frac{1}{4}\)
\(A_{min}=\frac{1}{4}\) khi \(\left\{{}\begin{matrix}a=\frac{1}{2}\\b=\frac{1}{2}\end{matrix}\right.\)


Xét \(a+b\ge1\Leftrightarrow b\ge1-a\)
Xét \(Q\ge\dfrac{8a^2+1-a}{4a}+\left(1-a\right)^2=\dfrac{8a^2}{4a}+\dfrac{1}{4a}-\dfrac{a}{4a}+1-2a+a^2\)
\(=2a+\dfrac{1}{4a}-\dfrac{1}{4}+1-2a+a^2\)\(=a^2+\dfrac{1}{4a}+\dfrac{3}{4}\)\(=\left(a^2+\dfrac{1}{8a}+\dfrac{1}{8a}\right)+\dfrac{3}{4}\)
Áp dụng Cosi được \(Q\ge3\sqrt[3]{a^2\cdot\dfrac{1}{8a}\cdot\dfrac{1}{8a}}+\dfrac{3}{4}\)\(=3\sqrt[3]{\dfrac{1}{64}}+\dfrac{3}{4}=\dfrac{3}{4}+\dfrac{3}{4}=\dfrac{3}{2}\)
Vậy \(Qmin=\dfrac{3}{2}\) khi \(a=b=\dfrac{1}{2}\)

Ta có: \(\frac{a}{1+4b^2}=\frac{a\left(1+4b^2\right)-4ab^2}{1+4b^2}=a-\frac{4ab^2}{1+4b^2}\ge a-\frac{4ab^2}{2\sqrt{4b^2.1}}=a-\frac{2ab^2}{2b}=a-ab\)(bđt cosi)
CMTT: \(\frac{b}{1+4a^2}\ge b-ab\)
=> P \(\ge a+b-2ab=4ab-2ab=2ab\)
Mặt khác ta có: \(a+b\ge2\sqrt{ab}\)(cosi)
=> \(4ab\ge2\sqrt{ab}\) <=> \(2ab\ge\sqrt{ab}\)<=> \(4a^2b^2-ab\ge0\) <=> \(ab\left(4ab-1\right)\ge0\)
<=> \(\orbr{\begin{cases}ab\le0\left(loại\right)\\ab\ge\frac{1}{4}\end{cases}}\)(vì a,b là số thực dương)
=> P \(\ge2\cdot\frac{1}{4}=\frac{1}{2}\)
Dấu "=" xảy ra <=> a = b = 1/2
Vậy MinP = 1/2 <=> a = b= 1/2
Ta có: \(a+b=4ab\le\left(a+b\right)^2\Leftrightarrow\left(a+b\right)\left[\left(a+b\right)-1\right]\ge0\)
Mà \(a+b>0\Rightarrow a+b\ge1\)
Áp dụng BĐT Cô-si, ta có: \(P=\frac{a}{1+4b^2}+\frac{b}{1+4a^2}=\left(a-\frac{4ab^2}{1+4b^2}\right)+\left(b-\frac{4a^2b}{1+4a^2}\right)\)\(\ge\left(a-\frac{4ab^2}{4b}\right)+\left(b-\frac{4a^2b}{4a}\right)=\left(a+b\right)-2ab=\left(a+b\right)-\frac{a+b}{2}=\frac{a+b}{2}\ge\frac{1}{2}\)
Đẳng thức xảy ra khi a = b = 1/2
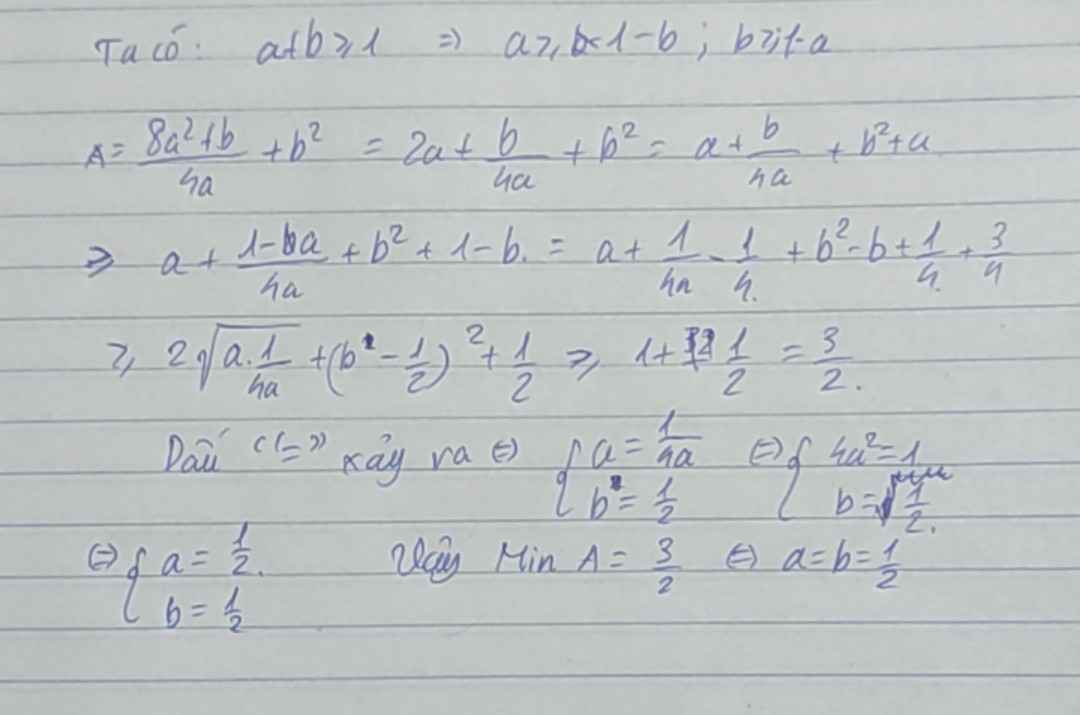
Bạn tham khảo:
Cho hai số thực a;b thay đổi thỏa mãn điều kiện \(a b\ge1\) và \(a>0\) Tìm GTNN của \(A=\frac{8a^2 b}{4a} b^2\) - Hoc24