Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A=2.(1/1.3 + 1/3.5 + 1/5.7 +.......+1/99.101)
=2.(1/1 + 1/3 + 1/5 + 1/5 + 1/7 +...+1/99 + 1/101)
=2.(1-1/101)
=2.(101/101-1/101)
=2.100/101
200/101
B=2.(1/1.3+1/3.5+1/3.1+....+1/99.101)
=2.(1/1+1/3+1/3+1/5+1/3+1/7+....+1/99+1/101)
=2.(1/1+1/101)
=2.(101/101+1/101)
=2.102/101
=204/101

\(A=\dfrac{2^4.3^3+2^3.3^4}{2^5.3^4-2^6.3^3}=\dfrac{2^3.3^3.\left(2+3\right)}{2^5.3^3.\left(3-2\right)}=\dfrac{2^3.3^3.5}{2^5.3^3.1}\)
\(=\dfrac{5}{2^2}=\dfrac{5}{4}\)

\(\dfrac{5}{3\cdot7}+\dfrac{5}{7\cdot11}+\dfrac{5}{11\cdot15}+...+\dfrac{5}{\left(4n-1\right)\left(4n+3\right)}\\ =\dfrac{5}{4}\cdot\left(\dfrac{4}{3\cdot7}+\dfrac{4}{7\cdot11}+\dfrac{4}{11\cdot15}+...+\dfrac{4}{\left(4n-1\right)\left(4n+3\right)}\right)\\ =\dfrac{5}{4}\cdot\left(\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{15}+...+\dfrac{1}{4n-1}-\dfrac{1}{4n+3}\right)\\ =\dfrac{5}{4}\cdot\left(\dfrac{1}{3}-\dfrac{1}{4n+3}\right)\\ =\dfrac{5}{4}\cdot\dfrac{4n}{12n+9}\\ =\dfrac{5n}{12n+9}\)
Mk thực sự nghĩ đề hình như bị sai hay sao ấy!

Còn một cái nữa là ta có thể so sánh với số trung gian như 1 và 0 .
Vì a/b=c/d khi a.c=b.d
Giờ thì mình kết thúc bài làm.

a: \(=\dfrac{1}{4}\cdot\dfrac{12}{5}\cdot\dfrac{100}{7}\cdot\dfrac{49}{100}\)
\(=\dfrac{1}{4}\cdot\dfrac{12}{5}\cdot\dfrac{49}{7}=\dfrac{3}{5}\cdot7=\dfrac{21}{5}\)
b: \(=\dfrac{3}{8}+\dfrac{1}{8}\cdot\dfrac{3}{4}-\dfrac{5}{4}\)
\(=\dfrac{12}{32}+\dfrac{3}{32}-\dfrac{40}{32}=\dfrac{-25}{32}\)
c: \(=\dfrac{4}{9}\left(\dfrac{-13}{27}-\dfrac{14}{27}\right)-\dfrac{5}{9}=\dfrac{-4}{9}-\dfrac{5}{9}=-1\)
d: \(=\dfrac{2}{4}\left(\dfrac{4}{3\cdot7}+\dfrac{4}{7\cdot11}+...+\dfrac{4}{91\cdot95}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+...+\dfrac{1}{91}-\dfrac{1}{95}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{92}{285}=\dfrac{46}{285}\)

a: \(\dfrac{5}{24}< \dfrac{15}{24}=\dfrac{5}{8}\)
b: \(\dfrac{6+9}{6\cdot9}=\dfrac{15}{54}\)
4/9=24/54
2/3=36/54
Do đó: \(\dfrac{15}{54}< \dfrac{24}{54}< \dfrac{36}{54}\)

a: 51/56=1-5/56
61/66=1-5/66
mà -5/56<-5/66
nên 51/56<61/66
b: 41/43<1<172/165
c: \(\dfrac{101}{506}>0>-\dfrac{707}{3534}\)

\(1,\)
\(\dfrac{45^2.3^8.10^5}{5^5.3^7.18^5}\)
\(=\dfrac{3^4.5^2.3^8.2^5.5^5}{5^5.3^7.2^5.3^{10}}\)
\(=\dfrac{3^{12}.2^5.5^7}{5^5.3^{17}.2^5}\)
\(=\dfrac{1.5^2}{3^5.1}\)
\(=\dfrac{25}{243}\)
\(2,\)
\(\dfrac{4^5.9^4+2.6^9}{2^{10}.3^8+6^8.20}\)
\(=\dfrac{2^{10}.3^8+2.2^9.3^9}{2^{10}.3^8+2^8.3^8.2^2.5}\)
\(=\dfrac{2^{10}.3^8+2^{10}.3^9}{2^{10}.3^8+2^{10}.3^8.5}\)
\(=\dfrac{2^{10}.3^8.4}{2^{10}.3^8.6}\)
\(=\dfrac{2^{12}.3^8}{2^{11}.3^9}\)
\(=\dfrac{2}{3}\)
\(3,\)
\(\dfrac{15.3^{11}+4.27^4}{9^7}\)
\(=\dfrac{3.5.3^{11}+2^2.3^{12}}{3^{14}}\)
\(=\dfrac{5.3^{12}+2^2.3^{12}}{3^{14}}\)
\(=\dfrac{3^{12}\left(5+2^2\right)}{3^{14}}\)
\(=\dfrac{3^{12}.9}{3^{14}}\)
\(=\dfrac{3^{14}}{3^{14}}\)
\(=1\)
\(4,\)
\(\dfrac{4^7.2^8}{3.2^{15}.16^2-5^2\left(2^{10}\right)^2}\)
\(=\dfrac{2^{22}}{3.2^{23}-5^2.2^{20}}\)
\(=\dfrac{2^{22}}{2^{20}.\left(-1\right)}\)
\(=\dfrac{2^{22}}{-2^{20}}\)
\(=-4\)
* Mấy bài còn lại tương tự đấy bạn tự làm đi
Mình mỏi tay lắm rồi
P/s:khuyến khích tự làm,chỉ làm mẫu 1 câu:
1)\(\dfrac{45^2.3^8.10^5}{5^5.3^7.18^5}=\dfrac{\left(5.9\right)^2.3.3^7.\left(2.5\right)^5}{5^5.3^7.\left(2.9\right)^5}\)\(=\dfrac{5^2.9^2.3.3^7.2^5.5^5}{5^5.3^7.2^5.9^5}\)\(=\dfrac{5^2.9^2.3.1.1.1}{1.1.1.9^5}\)\(=\dfrac{5^2.9^2.3}{9^5}=\dfrac{5^2.9^2.3}{9^2.9^3}=\dfrac{5^2.3}{9^3}=\dfrac{75}{729}=\dfrac{25}{243}\)
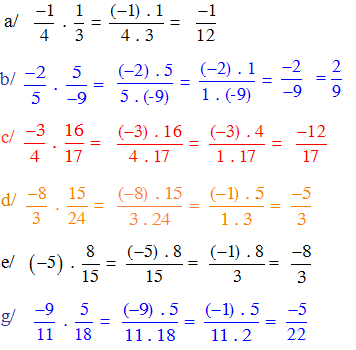
phân số thứ 2 ở trên tử số\(5^3\) thành \(5^2\) nha
\(\dfrac{a}{b}=\dfrac{3^4\cdot2^2\cdot\left(2-1\right)}{3^5\cdot\left(3^2-5\right)}=\dfrac{2^2}{3}\cdot\dfrac{1}{4}=\dfrac{1}{3}\)
\(\dfrac{c}{d}=\dfrac{5^3\left(7-2\right)}{5^3\left(7-4\right)}=\dfrac{5}{3}\)
Do đó: a/b<c/d