Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔAMB nội tiếp đường tròn
AB là đường kính
Do đó: ΔAMB vuông tại M

\(\text{a) Xét tứ giác ADMO có:}\)
∠DMO =90o (do M là tiếp tuyến của (O))
∠DAO =90o (do AD là tiếp tuyến của (O))
=> ∠DMO + ∠DAO = 180o
=> Tứ giác ADMO là tứ giác nội tiếp.
\(\text{b) Do D là giao điểm của 2 tiếp tuyến DM và DA nên OD là tia phân giác của ∠AOM}\)
=>(AOD = \(\frac{1}{2}\)∠AOM
Mặt khác ta có (ABM là góc nội tiếp chắn cung AM
=> ∠ABM = \(\frac{1}{2}\)∠AOM
=> ∠AOD = ∠ABM
Mà 2 góc này ở vị trí đồng vị
=> OD // BM
Xét tam giác ABN có:
OM// BM; O là trung điểm của AB
=> D là trung điểm của AN
c) Ta có: ΔOBM cân tại O ;OE ⊥MB =>OE là đường trung trực của MB
=>EM = EB => ΔMEB cân tại E => ∠EMB = ∠MEB (1)
ΔOBM cân tại O => ∠OMB = ∠OBM (2)
Cộng (1) và (2) vế với vế, ta được:
∠EMB + ∠OMB = ∠MEB + ∠OBM ⇔ ∠EMO =∠EOB ⇔ ∠EOB =90o
=>OB ⊥ BE
Vậy BE là tiếp tuyến của (O).
d) Lấy điểm E trên tia OA sao cho OE = \(\frac{OA}{3}\)
Xét tam giác OAI có OI vừa là đường cao vừa là trung tuyến
=> Tam giác OAI cân tại I => IA = IB; ∠IBA = ∠IAB
Ta có:
\(\hept{\begin{cases}\widehat{IBA}=\widehat{IAB}\\\widehat{IBA}+\widehat{INA}=90^0\\\widehat{NAI}+\widehat{IAB}=\widehat{NAB}=90^0\end{cases}}\)
=> ∠NAI = ∠INA => ΔINA cân tại I => IA = IN
Tam giác NAB vuông tại A có: IA = IN = IB
=> IA là trung tuyến của tam giác NAB
Xét ΔBNA có:
IA và BD là trung tuyến; IA ∩ BD = {J}
=> J là trọng tâm của tam giác BNA
Xét tam giác AIO có:
\(\frac{\text{AJ}}{AI}=\frac{AE}{A0}=\frac{2}{3}\Rightarrow\text{JE}\text{//}OI\)
=> J nằm trên đường thẳng d vuông góc với AB và cách O một khoảng bằng R/3.
Phần đảo: Lấy điểm J' bất kì thuộc đường thẳng d
Do d// OI (cùng vuông góc AB) nên ta có:
\(\frac{\text{AJ}}{AI}=\frac{AE}{A0}\)
\(\text{MÀ}\frac{AE}{AO}=\frac{2}{3}\Rightarrow\frac{\text{AJ}}{AI}=\frac{2}{3}\)
AI là trung tuyến của tam giác NAB
=> J' là trọng tâm tam giác NAB
Vậy khi M di chuyển trên (O) thì J di chuyển trên đường thẳng d vuông góc với AB và cách O một khoảng là R/3.
HÌNH Ở TRONG THỐNG KÊ HỎI ĐÁP NHA

E C M K I H A B O
a . Ta có : \(C\in\left(O\right),AB=2R\Rightarrow\widehat{ACB}=90^0\Rightarrow\Delta ABC\) vuông tại C
c . Vì \(OK\perp BC\Rightarrow B,C\) đối xứng qua OK
\(\Rightarrow\widehat{DCO}=\widehat{DBO}=90^0\Rightarrow DC\) là tiếp tuyến của (O)
d . Ta có \(AC=R\Rightarrow\Delta AOC\) đều
\(\Rightarrow\widehat{COM}=\widehat{MOB}=60^0\Rightarrow\Delta OCM,OMB\) đều
\(\Rightarrow OC=OM=OB=MB=MC\)=> ◊OBMC là hình thoi
e . Ta có :
\(\Delta ACO\) đều
\(\Rightarrow CH==\frac{R\sqrt{3}}{2}\Rightarrow CI=IH=\frac{R\sqrt{3}}{4}\)
\(\Rightarrow\frac{CI}{DB}=\frac{CI}{BC}=\frac{\frac{R\sqrt{3}}{4}}{R\sqrt{3}}=\frac{1}{4}=\frac{AH}{AB}=\frac{EI}{EB}\)
\(\Rightarrow\Delta ECI~\Delta EDB\left(c.g.c\right)\Rightarrow\widehat{CEI}=\widehat{DEB}\Rightarrow E,C,D\) thẳng hàng
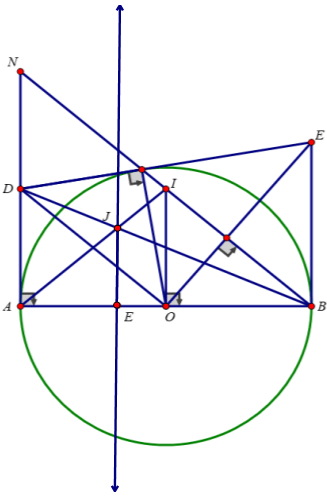
a.
Do AB là đường kính \(\Rightarrow\widehat{AMB}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{AMB}=90^0\Rightarrow\Delta AMB\) vuông tại M
b.
\(\widehat{AMK}=180^0-\widehat{AMB}=90^0\Rightarrow\Delta AMK\) vuông tại M
\(\Rightarrow MD\) là trung tuyến ứng với cạnh huyền
\(\Rightarrow MD=AD\)
Xét hai tam giác OAD và OMD có: \(\left\{{}\begin{matrix}OA=OM=R\\AD=MD\left(cmt\right)\\OD\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OAD=\Delta OMD\left(c.c.c\right)\)
\(\Rightarrow\widehat{OMD}=\widehat{OAD}=90^0\)
\(\Rightarrow DM\) là tiếp tuyến của (O).
c.
E là giao điểm 2 tiếp tuyến tại B và M \(\Rightarrow EM=EB\)
Mà \(OM=OB=R\Rightarrow OE\) là trung trực BM
\(\Rightarrow OE\) đồng thời là phân giác \(\widehat{BOM}\) hay \(\widehat{MOE}=\dfrac{1}{2}\widehat{BOM}\)
Tương tự ta có OD là phân giác \(\widehat{AOM}\Rightarrow\widehat{DOM}=\dfrac{1}{2}\widehat{AOM}\)
\(\Rightarrow\widehat{MOE}+\widehat{DOM}=\dfrac{1}{2}\left(\widehat{BOM}+\widehat{AOM}\right)\)
\(\Rightarrow\widehat{DOE}=\dfrac{1}{2}.180^0=90^0\)
Hay tam giác DOE vuông tại O
Áp dụng hệ thức lượng với đường cao OM:
\(DM.ME=OM^2\Leftrightarrow AD.BE=R^2\)