
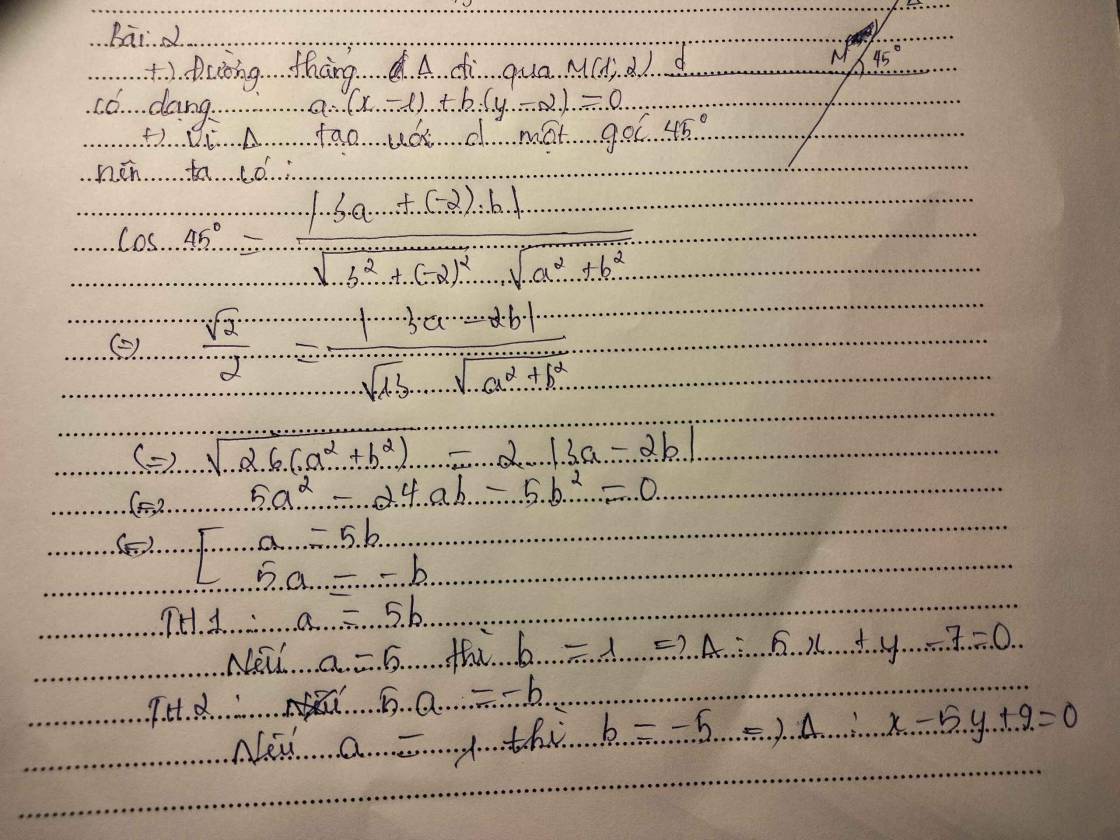

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

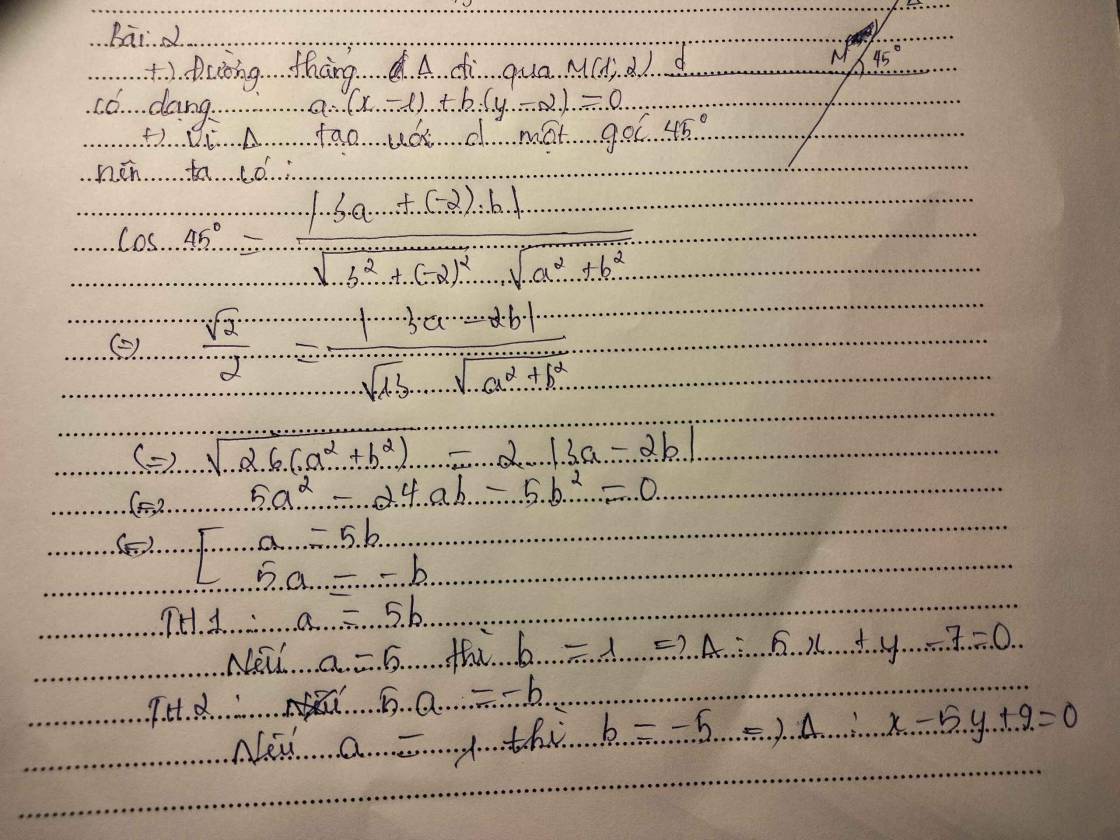


Vì hai đường thẳng \(\Delta \) và d song song với nhau nên ta có thể chọn \(\overrightarrow {{n_\Delta }} = \overrightarrow {{n_d}} = \left( {3; - 4} \right)\).
Mặt khác, \(\Delta \) đi qua điểm \(M\left( { - 1;2} \right)\)nên phương trình \(\Delta \) là:
\(3\left( {x + 1} \right) - 4\left( {y - 2} \right) = 0 \Leftrightarrow 3x - 4y + 11 = 0\).

gọi đường thẳng qua M là Δ có vecto n là (a;b) đk a2+b2 ≠ 0
PTTQ của đg đi qua M là a(x-1)+b(y-2)=0 *
ta có CT tính góc giữa hai 2 đt
cos (Δ ;d ) = \(\dfrac{\left|3a-2b\right|}{\sqrt{a^2+b^2}.\sqrt{3^2+\left(-2\right)^2}}=\dfrac{\sqrt{2}}{2}\)
\(2\left|3a-2b\right|=\sqrt{26}\sqrt{a^2+b^2}\)
\(4\left(9a^{2^{ }}+4b-12ab\right)=26\sqrt{a^2+b^2}\)
\(10a^2-48ab-10b^2=0\)
(hd bấm máy tính bạn bấm pt bậc 2 các hệ số lần lượt là a = 10 ,b=-48,c=-10 ra kq là x= 5 và -1:5 ròi ghi a=5b và a=-1:5b nha )
\(\left[{}\begin{matrix}a=5b\\a=-\dfrac{1}{5}b\end{matrix}\right.\)
th1 vs a=5b
chọn b=1 =>a =5 thế vào * => pt đt qua M (ở đây bạn thích chọn b= số nào cx đc nha mình chọn 1 vì tốn giản thôi ở dưới cx tương tự )
th2 vs a=-\(\dfrac{1}{5}\)b
chọn b=-5 => a = 1 thế vào * => pt đt qua M

a: Vì Δ//d nên Δ: 3x-4y+c=0
Thay x=1 và y=4 vào Δ, ta được:
c+3-16=0
=>c=13
b: Vì Δ vuông góc d nên Δ: 4x+3y+c=0
Thay x=-3 và y=-5 vào Δ, ta được:
c+4*(-3)+3(-5)=0
=>c-27=0
=>c=27
=>4x+3y+27=0

a.
Gọi \(M\left(x;y\right)\in d\)
\(\Rightarrow d\left(M;\Delta\right)=3\Leftrightarrow\dfrac{\left|3x-4y+6\right|}{\sqrt{3^2+4^2}}=3\)
\(\Leftrightarrow\left|3x-4y+6\right|=15\Rightarrow\left[{}\begin{matrix}3x-4y+21=0\\3x-4y-9=0\end{matrix}\right.\)
b.
Giả sử đường thẳng (d2) có dạng \(a\left(x+2\right)+b\left(y-3\right)=0\Leftrightarrow ax+by+2a-3b=0\) (1)
\(\dfrac{\left|3.a-4b\right|}{5\sqrt{a^2+b^2}}=\dfrac{1}{\sqrt{2}}\Leftrightarrow2\left(3a-4b\right)^2=25a^2+25b^2\)
\(\Leftrightarrow7a^2+48ab-7b^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}7a=b\\a=-7b\end{matrix}\right.\) \(\Rightarrow\left(a;b\right)=\left(1;7\right);\left(7;-1\right)\)
\(\Rightarrow...\) (bạn tự thế vào (1) và rút gọn)

Phương trình (d) có dạng :
ax + by + c = 0 (d)
=> vector pháp tuyến \(\overrightarrow{n}\left(a;b\right)\)
Lại có vector pháp tuyến của (d') : \(\overrightarrow{a}\left(1;2\right)\)
(d) qua A(0;1) => b + c = 0 (2)
Ta có \(\cos\left(d,d'\right)=\cos45=\dfrac{\left|a+2b\right|}{\sqrt{a^2+b^2}.\sqrt{1^2+2^2}}\)
\(\Leftrightarrow\left(a+2b\right)^2=\dfrac{5}{2}.\left(a^2+b^2\right)\)
\(\Leftrightarrow3a^2-8ab-3b^2=0\Leftrightarrow\left(a-3b\right).\left(3a+b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=3b\\a=-\dfrac{b}{3}\end{matrix}\right.\)\(\left(a;b\ne0\right)\) (1)
Từ (1)(2) thay vào (d) =>
d1 : 3x + y - 1 = 0
d2 : \(-\dfrac{1}{3}x+y-1=0\)