Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath

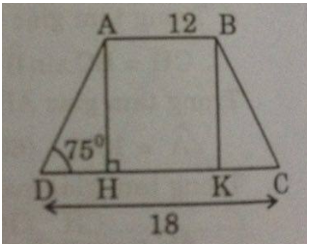
Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm, ˆD=75∘D^=75∘
Kẻ AH⊥CD,BK⊥CDAH⊥CD,BK⊥CD
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Ta có: tam giác ADH = tam giác BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK
Suy ra:
DH=CD–HK2=18–122=3(cm)DH=CD–HK2=18–122=3(cm)
Trong tam giác vuông ADH, ta có:
AH=DH.tgD=3.tg75∘≈11,196(cm)AH=DH.tgD=3.tg75∘≈11,196(cm)
Vậy:
SABCD=AB+CD2.AH≈12+182.11,196=167,94SABCD=AB+CD2.AH≈12+182.11,196=167,94 (cm2).

Câu 1:
Diện tích tam giác đều cạnh 3cm là:
\(S=\dfrac{3^2\cdot\sqrt{3}}{4}=\dfrac{9\sqrt{3}}{4}\left(cm^2\right)\)
Câu 2:
Nửa chu vi tam giác là:
\(P=\dfrac{C}{2}=\dfrac{8+8+6}{2}=\dfrac{22}{2}=11\left(cm\right)\)
Diện tích tam giác là:
\(S=\sqrt{P\cdot\left(P-A\right)\cdot\left(P-B\right)\cdot\left(P-C\right)}=\sqrt{11\cdot\left(11-8\right)^2\cdot\left(11-6\right)}\)
\(=\sqrt{11\cdot5\cdot9}=3\sqrt{55}\left(cm^2\right)\)