
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 26 trang 89 Sách Bài Tập (SBT) Toán Lớp 6 tập 2
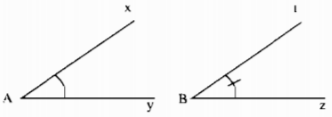
So sánh hai góc ở hình 10.
Hướng dẫn:
Cách 1: Đo riêng từng góc rồi so sánh hai số đó
Cách 2: Vẽ lại hai góc lên giấy trong. Đặt chồng hai góc sao cho đỉnh trùng nhau, một cạnh trùng nhau, hai cạnh còn lại của hai góc nằm cùng phía đối với cạnh trùng nhau rồi vận dụng kiến thức bài 5 để kết luận.
Giải
Dùng thước đo độ để đo hai góc ở hình 10 và so sánh.
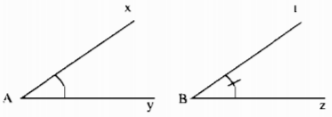
Tính tổng số đo hai góc trên hình 10.
Hướng dẫn:
Cách 1: Đo riêng từng góc rồi cộng hai số đo.
Cách 2: Vẽ hai góc ở vị trí kề nhau rồi đo góc tổng.
Giải
Sử dụng thước đo độ sau đó cộng số đo hai góc.
a) Vẽ góc có đỉnh là M trên giấy cứng. Cắt ra ta được một mẫu hình.
b) Đóng hai chiếc đinh vào hai điểm A và B cách nhau 2,5 cm. Đưa mẫu hình vào khe hở giữa hai chiếc đinh sao cho một cạnh sát A, một cạnh sát B. Khi đó đỉnh M của góc ở vị trí \(M_1\). Đặt mẫu hình nhiều lần để được nhiều vị trí \(M_1,M_2,M_3\).. khác nhau của đỉnh M. Vậy ta có:
\(\widehat{AM_1B}=\widehat{AM_2B}=\widehat{AM_3B}=...=40^o\)
Đánh dấu khoảng 10 vị trí khác nhau của đỉnh M và dự đoán quỹ đạo của đỉnh M (hình 11)

Giải
b) Quỹ đạo của điểm M được gọi là "cung chứa góc \(40^o\)
Bài 29 tự làm,có trong sách mà bạn
Bài 26 trang 89 Toán 6
So sánh hai góc ở hình 10.

Hướng dẫn: Cách 1: Đo riêng từng góc rồi so sánh hai số đó
Cách 2: Vẽ lại hai góc lên giấy trong. Đặt chồng hai góc sao cho đỉnh trùng nhau, một cạnh trùng nhau, hai cạnh còn lại của hai góc nằm cùng phía đối với cạnh trùng nhau rồi vận dụng kiến thức bài 5 để kết luận.
Giải: Dùng thước đo độ để đo hai góc ở hình 10 và so sánh.
Bài 27 trang 89
Tính tổng số đo hai góc trên hình 10.
Hướng dẫn:
Cách 1: Đo riêng từng góc rồi cộng hai số đo.
Cách 2: Vẽ hai góc ở vị trí kề nhau rồi đo góc tổng.

Giải: Sử dụng thước đo độ sau đó cộng số đo hai góc.
Bài 28 Toán 6
a) Vẽ góc có đỉnh là M trên giấy cứng. Cắt ra ta được một mẫu hình.
b) Đóng hai chiếc đinh vào hai điểm A và B cách nhau 2,5 cm. Đưa mẫu hình vào khe hở giữa hai chiếc đinh sao cho một cạnh sát A, một cạnh sát B. Khi đó đỉnh M của góc ở vị trí M1M1. Đặt mẫu hình nhiều lần để được nhiều vị trí M1,M2,M3M1,M2,M3, … khác nhau của đỉnh M. Vậy ta có:
ˆAM1B=ˆAM2B=ˆAM3B=…=400AM1B^=AM2B^=AM3B^=…=400
Đánh dấu khoảng 10 vị trí khác nhau của đỉnh M và dự đoán quỹ đạo của đỉnh M (hình 11)

HD: b) Quỹ đạo của điểm M được gọi là “cung chứa góc 400400.
29a) Ta có hình vẽ

b) Vì ˆARNARN^ và ˆSRNSRN^ kề bù nên:
ˆARN+ˆSRN=180OARN^+SRN^=180O
Thay ˆSRN=130OSRN^=130O ta có:
ˆARN+130O=180OARN^+130O=180O
⇒ˆARN=180O–130O=50O⇒ARN^=180O–130O=50O
Vì ˆARMARM^ và ˆMRSMRS^ kề bù nên:
ˆARM+ˆMRS=180OARM^+MRS^=180O
Thay ˆARM=130OARM^=130O ta có:
130O+ˆMRS=180O130O+MRS^=180O
⇒ˆMRS=180O–130O=50O⇒MRS^=180O–130O=50O
Vì hai tia RN và RM nằm trên cùng môt nửa mặt phẳng bờ chứa tia RA
ˆARN=50O;ˆARM=130OARN^=50O;ARM^=130O suy ra ˆARN<ˆARMARN^<ARM^
Nên tia RN nằm giữa hai tia RA và RM
⇒ˆARN+ˆMRN=ˆARM⇒ARN^+MRN^=ARM^. Thay ˆARN=50O;ˆARM=130OARN^=50O;ARM^=130O ta có:
50O+ˆMRN=130O50O+MRN^=130O
⇒ˆMRN=130O–50O=80O

Dễ mà. Hai số giống nhau. Có nghĩa là bên dưới thế nào bên trên cũng số đó, và ngược lại.

Bài 11
Từ hình vẽ, ta có thể điền như sau:
a) Điểm R nằm giữa hai điểm M và N.
b) Hai điểm R và N nằm cùng phía đối với điểm M.
c) Hai điểm M và N nằm khác phía đối với R.
Bài 12

a) điểm N nằm giữa 2 điểm M và P.
b, điểm M không nằm giữa hai điểm N và Q.
c, điểm N và P nằm giữa hai điểm M và Q.
Bài 13
a, Điểm M nằm giữa hai điểm A và B; điểm N không nằm giữa hai điểm A và B (Ba điểm N,A,B thẳng hàng)
nên cả 4 điểm này cùng thẳng hàng (cùng nằm trên một đường thẳng).
Chúng ta có hai cách vẽ:
Cách 1:
Cách 2:
b) Điểm B nằm giữa A và N; điểm M nằm giữa hai điểm A và B.
Điểm B nằm giữa hai điểm A và N nên 3 điểm B, A, N thẳng hàng.
Điểm M nằm giữa hai điểm A và B nên 3 điểm B, A, M thẳng hàng.
Do đó, cả 4 điểm A, B, M, N đều thẳng hàng (cùng nằm trên một đường thẳng).
Bài 11
a) Điểm R nằm giữa 2 điểm M và N
b) 2 điểm R và N nằm cùng phía đối với điểm M
c) 2 điểm M và N nằm khác phía đối với R
Bài 12
a) Điểm M nằm giữa 2 điểm M và P
b) Điểm M ko nằm giữa 2 điểm N và Q
c) Điểm N và P nằm giữa 2 điểm M và Q
Bài 13
a) AMBN
b) Vẽ giống hình câu a

Bài 70. ( trang 30 ) Viết các số: 987; 2564; abcde dưới dạng tổng các lũy thừa của 10.
Bài 73 : ( trang 32 )Giải: 987 = 9 . 102 + 8 . 10 + 7;
2564 = 2 . 103 + 5 . 102 + 6 . 10 + 4;
abcde= a . 104 + b . 103 + c . 102 + d . 10 + e
a) 5 . 42 – 18 : 32 = 5 . 16 - 18 : 9 = 80 - 2 = 78;
b) 33 . 18 – 33 . 12 = 27 . 18 - 27 . 12 = 486 - 324 = 162;
Lưu ý. Có thể áp dụng tính chất phân phối của phép nhân đối với phép cộng như sau:
33 . 18 – 33 . 12 = 33 (18 - 12) = 27 . 6 = 162;
c) 39 . 213 + 87 . 39 = 39 . (213 + 87) = 39 . 300 = 11700;
d) 80 – [130 – (12 – 4)2] = 80 - (130 - 82) = 80 - (130 - 64) = 80 - 66 = 14.
Bài 74 ( trang 32 ) a) 541 + (218 - x) = 735
Suy ra 218 - x = 735 - 541
218 - x = 194.
x = 218 - 194.
Vậy x = 24.
b) 5(x + 35) = 515
suy ra x + 35 = 515 : 5
x + 35 = 103.
x = 103 - 35 =68.
c) Từ 96 - 3(x + 1) = 42
suy ra 3(x + 1) = 96 - 42
3(x + 1)= 54.
x + 1 = 18.
x = 18 - 1
Vậy x = 17.
d) Từ 12x - 33 = 32 . 33
12x - 33 = 243
12x = 243 + 33
12x = 276
x = 276 : 12
Vậy x = 23.
Ko bt có phải bài bạn cần ko nx nhưng mong nó giúp được bn
Hok tốt
# MissyGirl #

73 là số nguyên tố
Các số 1431 ; 635 ; 119 là hợp số vì chúng có các ước 3,5,7


Viết đầu bài ra đi bạn muốn trả lời mà viết thế này hả
bạn chỉ cần tìm các số \(\in Z\)là đc xong rùi thì tính tổng cọng hết vào