Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo giả thiết ta có 3 góc: \(\alpha;\beta=\alpha+\dfrac{\pi}{3};\gamma=\alpha+\dfrac{2\pi}{3}\).
Ta có:
\(tan\alpha.tan\left(\alpha+\dfrac{\pi}{3}\right)+tan\left(\alpha+\dfrac{\pi}{3}\right).tan\left(\alpha+\dfrac{2\pi}{3}\right)+\)\(tan\left(\alpha+\dfrac{2\pi}{3}\right).tan\alpha\)
\(=tan\alpha\left[tan\left(\alpha+\dfrac{\pi}{3}\right)+tan\left(\alpha+\dfrac{2\pi}{3}\right)\right]\)\(+tan\left(a+\dfrac{\pi}{3}\right)tan\left(\alpha+\dfrac{2\pi}{3}\right)\)
\(=tan\alpha\dfrac{sin\left(2\alpha+\pi\right)}{cos\left(\alpha+\dfrac{\pi}{3}\right)cos\left(\alpha+\dfrac{2\pi}{3}\right)}\)\(+\dfrac{sin\left(\alpha+\dfrac{\pi}{3}\right)sin\left(\alpha+\dfrac{2\pi}{3}\right)}{cos\left(\alpha+\dfrac{\pi}{3}\right)cos\left(\alpha+\dfrac{2\pi}{3}\right)}\)
\(=tan\alpha\dfrac{-sin2\alpha}{cos\left(\alpha+\dfrac{\pi}{3}\right)cos\left(\alpha+\dfrac{2\pi}{3}\right)}\)\(+\dfrac{cos\dfrac{\pi}{3}-cos\left(2\alpha+\pi\right)}{2cos\left(\alpha+\dfrac{\pi}{3}\right)cos\left(\alpha+\dfrac{2\pi}{3}\right)}\)
\(=\dfrac{-2sin^2\alpha}{cos\left(\alpha+\dfrac{\pi}{3}\right)cos\left(\alpha+\dfrac{2\pi}{3}\right)}\)\(+\dfrac{\dfrac{1}{2}+cos2\alpha}{2cos\left(\alpha+\dfrac{\pi}{3}\right)cos\left(\alpha+\dfrac{2\pi}{3}\right)}\)
\(=\dfrac{\dfrac{1}{2}-4sin^2\alpha+cos2\alpha}{2cos\left(\alpha+\dfrac{\pi}{3}\right)cos\left(\alpha+\dfrac{2\pi}{3}\right)}\)
\(=\dfrac{\dfrac{1}{2}-4\left(1-cos^2\alpha\right)+2cos^2\alpha-1}{cos\dfrac{\pi}{3}+cos\left(2\alpha+\pi\right)}\)
\(=\dfrac{6cos^2\alpha-\dfrac{9}{2}}{\dfrac{1}{2}-cos2\alpha}\)
\(=\dfrac{3\left(2cos^2\alpha-\dfrac{3}{2}\right)}{\dfrac{1}{2}-\left(2cos^2\alpha-1\right)}=\dfrac{3\left(2cos^2\alpha-\dfrac{3}{2}\right)}{\dfrac{3}{2}-2cos^2\alpha}=-3\).
\(4cos\alpha.cos\beta cos\gamma=4cos\alpha cos\left(\alpha+\dfrac{\pi}{3}\right)cos\left(\alpha+\dfrac{2\pi}{3}\right)\)
\(=4cos\alpha.\dfrac{1}{2}\left(cos\dfrac{\pi}{3}+cos\left(2\alpha+\pi\right)\right)\)
\(=4cos\alpha.\dfrac{1}{2}\left(\dfrac{1}{2}-cos2\alpha\right)\)
\(=cos\alpha-2cos\alpha.cos2\alpha\)
\(=cos\alpha-\left(cos\alpha+cos3\alpha\right)\)
\(=-cos3\alpha\)
\(=cos\left(\pi+3\alpha\right)\)
\(=cos3\left(\dfrac{\pi}{3}+\alpha\right)\)
\(=cos3\beta\) (đpcm).

+) Xét \(\beta = - \alpha \), khi đó:
\(\begin{array}{l}cos\beta = cos\left( {-{\rm{ }}\alpha } \right) = cos\alpha ;\\sin\beta = sin\left( {-{\rm{ }}\alpha } \right) = -sin\alpha \Leftrightarrow sin\alpha = -sin\beta .\end{array}\)
Do đó A thỏa mãn.
Đáp án: A

\(a)\;sin(\alpha + \beta ).sin(\alpha - \beta ) = \;\frac{1}{2}.\left[ {cos\left( {\alpha + \beta - \alpha + \beta } \right) - cos\left( {\alpha + \beta + \alpha - \beta } \right)} \right]\)
\(\begin{array}{l} = \;\frac{1}{2}.(cos2\beta - cos2\alpha ) = \;\frac{1}{2}.(1 - 2si{n^2}\beta - 1 + 2si{n^2}\alpha )\\ = si{n^2}\alpha - si{n^2}\beta \end{array}\)
\(\begin{array}{l}b)\;co{s^4}\alpha - co{s^4}\left( {\alpha - \frac{\pi }{2}} \right) = \;co{s^4}\alpha - si{n^4}\alpha \\ = \;(co{s^2}\alpha + si{n^2}\alpha )(co{s^2}\alpha - si{n^2}\alpha )\\ = \;co{s^2}\alpha -si{n^2}\alpha = cos2\alpha .\end{array}\)

Ta có:
A. \(\alpha< \beta\)
\(\Rightarrow\left(0,3\right)^{\alpha}>\left(0,3\right)^{\beta}\)
Sai
B. \(\alpha< \beta\)
\(\Rightarrow\pi^{\alpha}< \pi^{\beta}\)
Sai
C. \(\alpha< \beta\)
\(\Rightarrow\left(\sqrt{2}\right)^{\alpha}< \left(\sqrt{2}\right)^{\beta}\)
Đúng
D. \(\alpha< \beta\)
\(\Rightarrow\left(\dfrac{1}{2}\right)^{\alpha}>\left(\dfrac{1}{2}\right)^{\beta}\)
Sai
⇒ Chọn C
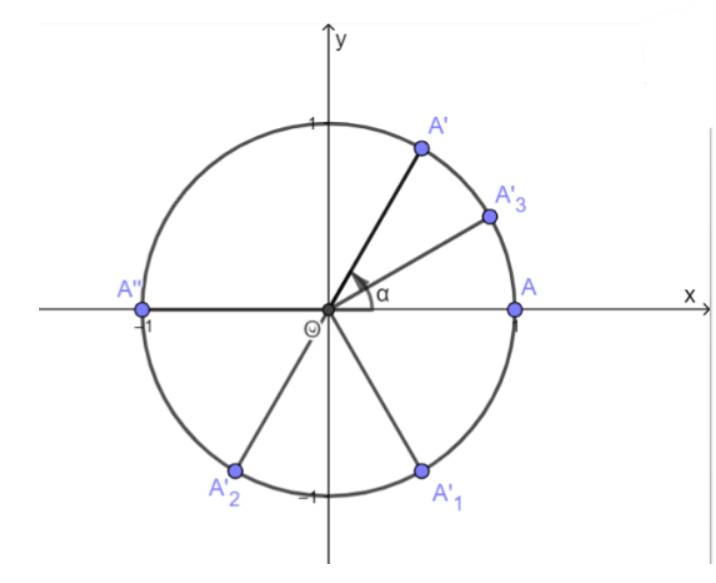
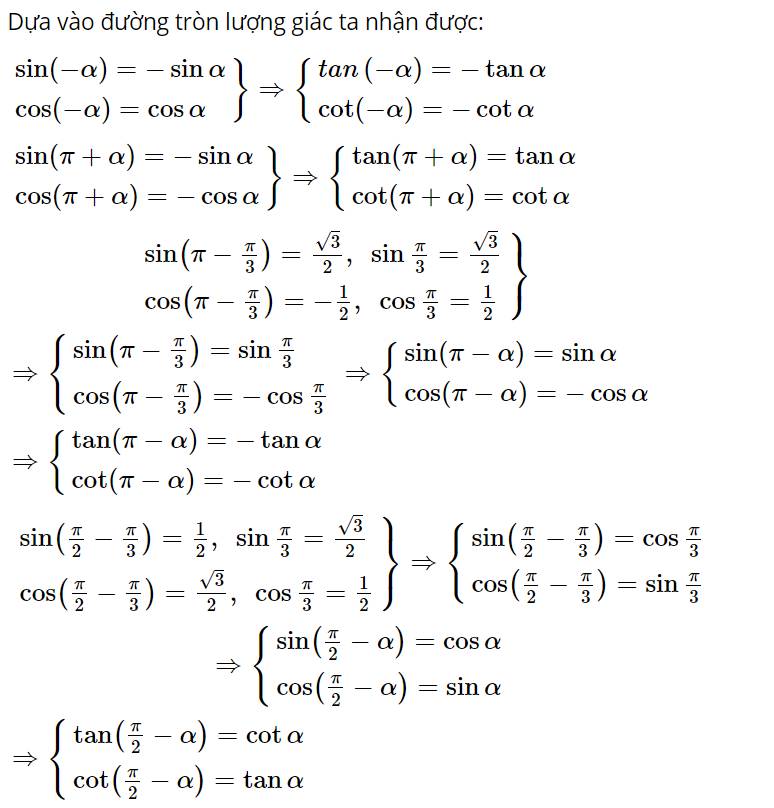
Ta có: \(\frac{{25\pi }}{3} = \frac{\pi }{3} + 4.2\pi .\) Do đó điểm biểu diễn cung lượng giác \(\frac{{25\pi }}{3}\) trùng với điểm biểu diễn cung lượng giác \(\frac{\pi }{3}\).
Vậy ta chọn đáp án A