Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

TH1: `m=0 `
`2x>0 <=> x>0`
`=>` Không thỏa mãn.
TH2: `m>0`
Bất PT có tập nghiệm là `RR <=> \Delta'<0`
`<=> (m-1)^2-m.4m<0`
`<=> m<-1 ; 1/3 <m`
Vậy `m in (0;+∞)` thỏa mãn.
TH1 là m=0 thì TH2 là \(m\ne0\)
Bpt có tập nghiệm là R <=> \(\left\{{}\begin{matrix}a>0\\\Delta'< 0\end{matrix}\right.\)
Đáp án: m\(\in\left(\dfrac{1}{3};+\infty\right)\)

Ta có 2x – 4 >0
* Xét bất phương trình: mx – 1 <0 (*)
+ Nếu m = 0 thì ( *) luôn đúng với mọi x.
Khi đó, tập nghiệm của hệ bất phương trình là ( 2 ; + ∞ ) .
+ Nếu m > 0 thì từ (*) ⇔ m x < 1 ⇔ x < 1 m
Trong trường hợp này thì tập nghiệm của hệ bất phương trình không thể là ( 2 ; + ∞ ) .
+ Nếu m < 0 thì từ (*) ⇔ m x < 1 ⇔ x < 1 m
Do đó, để hệ bất phương trình đã cho có tập nghiệm là ( 2 ; + ∞ ) khi và chỉ khi 1 m < 2 ( luôn đúng vì m < 0).
Vậy tập hợp các giá trị m thỏa mãn là m ≤ 0 .

Ta có: 2 x - 1 > 0 ⇔ 2 x > 1 ⇔ x > 1 2
* Xét bất phương trình mx – 3 < 0 (*)
+ Nếu m = 0 thì (*) luôn đúng với mọi x. khi đó, nghiệm của hệ bất phương trình là: 1 2 ; + ∞
+ Nếu m < 0 thì (*): m x < 3 ⇔ x > 3 m
Khi đó, tập nghiệm của hệ bất phương trình là: m a x 1 2 ; 3 m ; + ∞
+ Nếu m >0 thì (*) m x < 3 ⇔ x < 3 m
Để hệ bất phương trình có tập nghiệm là khoảng 1 2 ; 2 thì 3 m = 2 ⇔ m = 3 2
Kết luận: Để hệ bất phương trình có tập nghiệm là khoảng 1 2 ; 2 thì m = 3 2

Đáp án: B
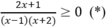
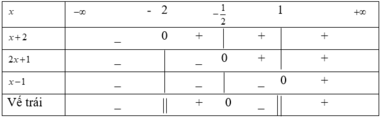
Ta có bảng xét dấu vế trái của (*):
Từ đó suy ra tập nghiệm của (*) là:
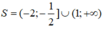
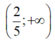
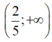
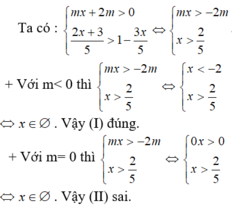
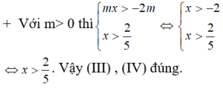
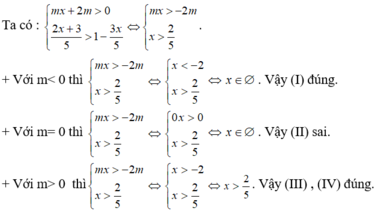
Bất phương trình \(x^2+2x+m-5\ge0\) có tập nghiệm là \((-\infty;3]\) có nghiệm khi \(m\in[2;+\infty)\)