Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC có DE//BC
nên \(\dfrac{AD}{AB}=\dfrac{DE}{BC}\)
=>\(\dfrac{DE}{8}=\dfrac{2}{5}\)
=>\(DE=2\cdot\dfrac{8}{5}=\dfrac{16}{5}=3,2\left(cm\right)\)

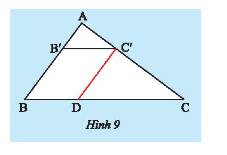
a) Xét tam giác \(ABC\) có \(B'C'//BC\) nên theo định lí Thales ta có:
\(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{2}{6} = \frac{{AC'}}{8}\). Do đó, \(AC' = \frac{{2.8}}{6} = \frac{8}{3}\left( {cm} \right)\).
Vậy \(AC' = \frac{{16}}{3}cm\).
b) Xét tam giác \(ABC\) có \(C'D//AB\) nên theo định lí Thales ta có:
\(\frac{{BD}}{{BC}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{{BD}}{{10}} = \frac{{\frac{8}{3}}}{8}\). Do đó, \(BD = \frac{{10.\frac{8}{3}}}{8} = \frac{{10}}{3}\left( {cm} \right)\).
Vậy \(BD = \frac{{10}}{3}cm\).
Ta có: \(BB' = AB - AB' = 6 - 2 = 4cm\)
Vì \(\left\{ \begin{array}{l}B'C'//BC\\C'D//AB\end{array} \right. \Rightarrow \left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right.\) (do \(D \in BC;B' \in AB\))
Xét tứ giác \(B'C'DB\) có
\(\left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right. \Rightarrow \) tứ giác \(B'C'DB\) là hình bình hành (dấu hiệu nhận biết)
\( \Rightarrow \left\{ \begin{array}{l}B'C' = BD = \frac{{10}}{3}cm\\BB' = C'D = 4cm\end{array} \right.\) (tính chất hình bình hành)
c) Ta có: \(\frac{{AB'}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AC'}}{{AC}} = \frac{{\frac{8}{3}}}{8} = \frac{1}{3};\frac{{BC'}}{{BC}} = \frac{{\frac{{10}}{3}}}{{10}} = \frac{1}{3}\)
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{{B'C'}}{{BC}}\).

AB=AD+DF+FB
AC=AE+EG+GC
TAM GIÁC ABC=AD+DF+FB+AE+EG+GC
MÀ AD=DF=FB
SUY RA AE=EG=GC
* AD=DF
AE=EG
FD=FB
GE=GC
SUY RA DE ,FG LÀ ĐTB TAM GIÁC ABC
SUY RA DE=1/2 BC
FG=1/2 BC
SUY RA DE+FG=BC
B. DE=FG=1/2BC
SUY RA DE=FG=1/2X9=4.5cm
AB=AD+DF+FB
AC=AE+EG+GC
TAM GIÁC ABC=AD+DF+FB+AE+EG+GC
MÀ AD=DF=FB
SUY RA AE=EG=GC
* AD=DF
AE=EG
FD=FB
GE=GC
SUY RA DE ,FG LÀ ĐTB TAM GIÁC ABC
SUY RA DE=1/2 BC
FG=1/2 BC
SUY RA DE+FG=BC
B. DE=FG=1/2BC
SUY RA DE=FG=1/2X9=4.5cm

a) +)Xét tg ABD có: CE //BD(gt)
Áp dụng đl Ta-let, ta có:
AB/AC=AD/AE
+) Xét tam giác ADC có: FE // CD(gt)
Áp dụng đl Ta-let,ta có:
AC/AF=AD/AE
b)Từ câu a), ta có:
AB/AC=AC/AF
->AC.AC=AB.AF
->AC^2=AB.AF

Tự vẽ hình.
a) Xét tam giác OAB có AB // CD
⇒AOOC=OBOD=ABDC⇒12OC=93=18DC⇒AOOC=OBOD=ABDC⇒12OC=93=18DC ( Hệ quả định lý Ta - lét ) (1)
=> OC = 4cm, DC = 6cm
Vậy OC = 4cm và DC = 6cm
b) Xét tam giác FAB có DC // AB
⇒FDAD=FCCB⇒FD.BC=FC.AD⇒FDAD=FCCB⇒FD.BC=FC.AD ( ĐPCM )
c) Theo (1), ta đã có:
OAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBDOAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBD (2)
Vì MN // AB mà AB // DC => MN // DC
Xét tam giác ADC có MO// DC
⇒MODC=AOAC⇒MODC=AOAC ( Hệ quả định lý Ta - lét ) (3)
CMTT : ONDC=OBDBONDC=OBDB (4)
Từ (2), (3) và (4) => MODC=NODC⇒MO=NOMODC=NODC⇒MO=NO ( ĐPCM )

Dễ thôi:vvv
a) Vì DF//AC
=> \(\dfrac{AF}{AB}=\dfrac{CD}{BC}=\dfrac{2}{1+2}=\dfrac{2}{3}\)
Vì DE//AB
=> \(\dfrac{AE}{AC}=\dfrac{BD}{BC}=\dfrac{1}{1+2}=\dfrac{1}{3}\)
b) Ta có: \(\dfrac{AE}{AC}=\dfrac{1}{3}\Leftrightarrow\dfrac{AE}{2AM}=\dfrac{1}{3}\Leftrightarrow\dfrac{AE}{AM}=\dfrac{2}{3}\)
Lại có: \(\dfrac{AF}{AB}=\dfrac{2}{3}\)
=> \(\dfrac{AF}{AB}=\dfrac{AE}{AM}\)
=> EF//BM(theo đ/lý Ta-lét đảo)

434
AI TICK GIÙM MÌNH MỘT CÁI ĐI MÀ LÀM ƠN ĐÓ!!!!!!!!!!!!!!!!!!!!!!!
1: Xét ΔABC có DE//BC
nên AE/AC=AD/AB
=>AE/8=1/3
=>AE=8/3(cm)
2:
Xét ΔABC có DE//BC
nên DE/BC=AD/AB
=>DE/10=1/3
=>DE=10/3(cm)
Xét tứ giác BDEF có
BD//EF
BF//DE
Do đó: BDEF là hình bình hành
=>BF=DE=10/3(cm)
3:
AD/AB=1/3
AE/AC=1/3
DE/BC=1/3
Do đó: AD/AB=AE/AC=DE/BC