Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1: (1/2x - 5)20 + (y2 - 1/4)10 < 0 (1)
Ta có: (1/2x - 5)20 \(\ge\)0 \(\forall\)x
(y2 - 1/4)10 \(\ge\)0 \(\forall\)y
=> (1/2x - 5)20 + (y2 - 1/4)10 \(\ge\)0 \(\forall\)x;y
Theo (1) => ko có giá trị x;y t/m
Bài 2. (x - 7)x + 1 - (x - 7)x + 11 = 0
=> (x - 7)x + 1.[1 - (x - 7)10] = 0
=> \(\orbr{\begin{cases}\left(x-7\right)^{x+1}=0\\1-\left(x-7\right)^{10}=0\end{cases}}\)
=> \(\orbr{\begin{cases}x-7=0\\\left(x-7\right)^{10}=1\end{cases}}\)
=> x = 7
hoặc : \(\orbr{\begin{cases}x-7=1\\x-7=-1\end{cases}}\)
=> x = 7
hoặc : \(\orbr{\begin{cases}x=8\\x=6\end{cases}}\)
Bài 3a) Ta có: (2x + 1/3)4 \(\ge\)0 \(\forall\)x
=> (2x +1/3)4 - 1 \(\ge\)-1 \(\forall\)x
=> A \(\ge\)-1 \(\forall\)x
Dấu "=" xảy ra <=> 2x + 1/3 = 0 <=> 2x = -1/3 <=> x = -1/6
Vậy Min A = -1 tại x = -1/6
b) Ta có: -(4/9x - 2/5)6 \(\le\)0 \(\forall\)x
=> -(4/9x - 2/15)6 + 3 \(\le\)3 \(\forall\)x
=> B \(\le\)3 \(\forall\)x
Dấu "=" xảy ra <=> 4/9x - 2/15 = 0 <=> 4/9x = 2/15 <=> x = 3/10
vậy Max B = 3 tại x = 3/10

Bài 1: Sử dụng phép thế
Có x - y = 2 => x = 2 + y
Thay x = 2 + y vào các biểu thức cần tính
Bài 2:
\(P=9-2\left|x-3\right|\le9\) dấu bằng <=> x = 3
\(Q=\left|x-2\right|+\left|x-8\right|=\left|x-2\right|+\left|8-x\right|\ge\left|x-2+8-x\right|=6\) dấu bằng <=> \(\left(x-2\right)\left(8-x\right)\ge0\)

Bài 1 và 2 dễ rồi bạn tự làm được
Bài 3 :
\(a)\) Ta có :
\(\left|2x+3\right|\ge0\)
Mà \(\left|2x+3\right|=x+2\)
\(\Rightarrow\)\(x+2\ge0\)
\(\Rightarrow\)\(x\ge-2\)
Trường hợp 1 :
\(2x+3=x+2\)
\(\Leftrightarrow\)\(2x-x=2-3\)
\(\Leftrightarrow\)\(x=-1\) ( thoã mãn )
Trường hợp 2 :
\(2x+3=-x-2\)
\(\Leftrightarrow\)\(2x+x=-2-3\)
\(\Leftrightarrow\)\(3x=-5\)
\(\Leftrightarrow\)\(x=\frac{-5}{3}\) ( thoã mãn )
Vậy \(x=-1\) hoặc \(x=\frac{-5}{3}\)
Chúc bạn học tốt ~

Bài 3 :
Vì \(\left(x-2\right)^2\ge0\forall x\)
Nên : \(A=\left(x-2\right)^2-4\ge-4\forall x\)
Vậy \(A_{min}=-4\) khi x = 2
B1: lấy máy tính mà tính thôi bạn (nhớ lm theo từng bước)
B2:
a, \(\left|x-\frac{2}{3}\right|-\frac{1}{2}=\frac{5}{6}\)
\(\left|x-\frac{2}{3}\right|=\frac{4}{3}\)
\(\Rightarrow\orbr{\begin{cases}x-\frac{2}{3}=\frac{4}{3}\\x-\frac{2}{3}=\frac{-4}{3}\end{cases}\Rightarrow\orbr{\begin{cases}x=2\\x=\frac{-2}{3}\end{cases}}}\)
b, \(\frac{\left(-2\right)^x}{512}=-32\Rightarrow\left(-2\right)^x=-16384\Rightarrow x\in\varnothing\)
B3:
Vì \(\left(x-2\right)^2\ge0\Rightarrow A=\left(x-2\right)^2-4\ge-4\)
Dấu "=" xảy ra khi x = 2
Vậy GTNN của A = -4 khi x = 2

Bài 2:
a: \(x^2+2>=2\)
\(\Leftrightarrow\dfrac{8}{x^2+2}< =4\)
\(\Leftrightarrow B>=-4\)
Dấu '=' xảy ra khi x=0
b: \(4+2\left(x-2\right)^2>=4\)
=>C=1/4+2(x-2)^2<=1/4
Dấu '=' xảy ra khi x=2
Bài 3:
a: \(\Leftrightarrow\dfrac{x+5-x+3}{x-3}< 0\)
=>x-3<0
=>x<3
b: \(\Leftrightarrow\dfrac{x+3-2x-8}{x+4}>0\)
\(\Leftrightarrow\dfrac{-x-5}{x+4}>0\)
=>(x+5)/(x+4)<0
=>-5<x<-4
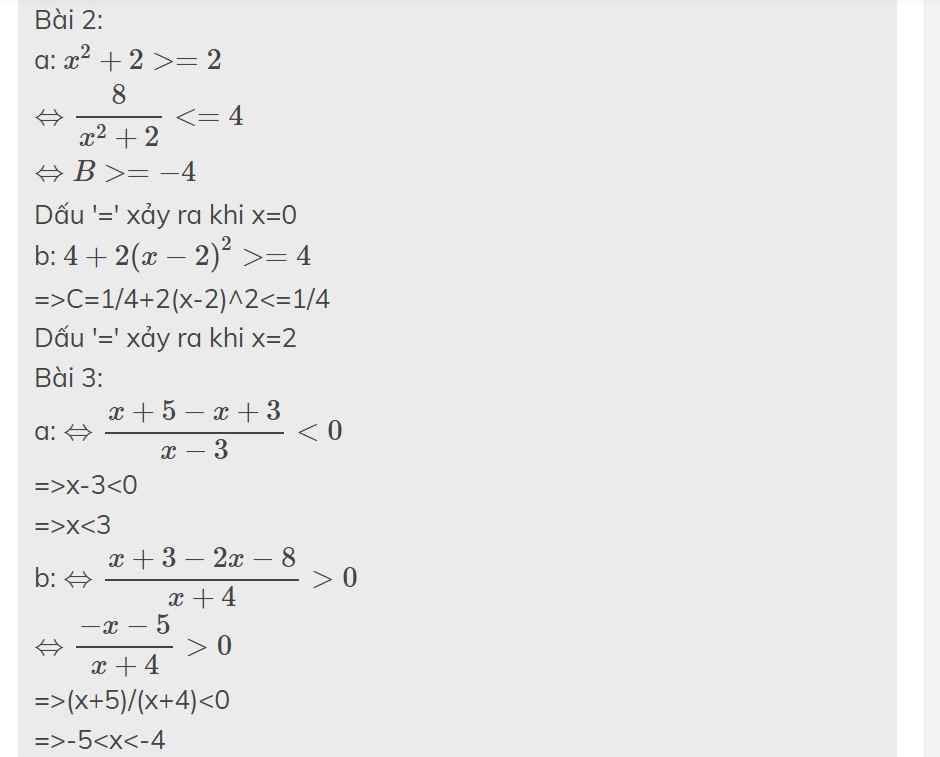
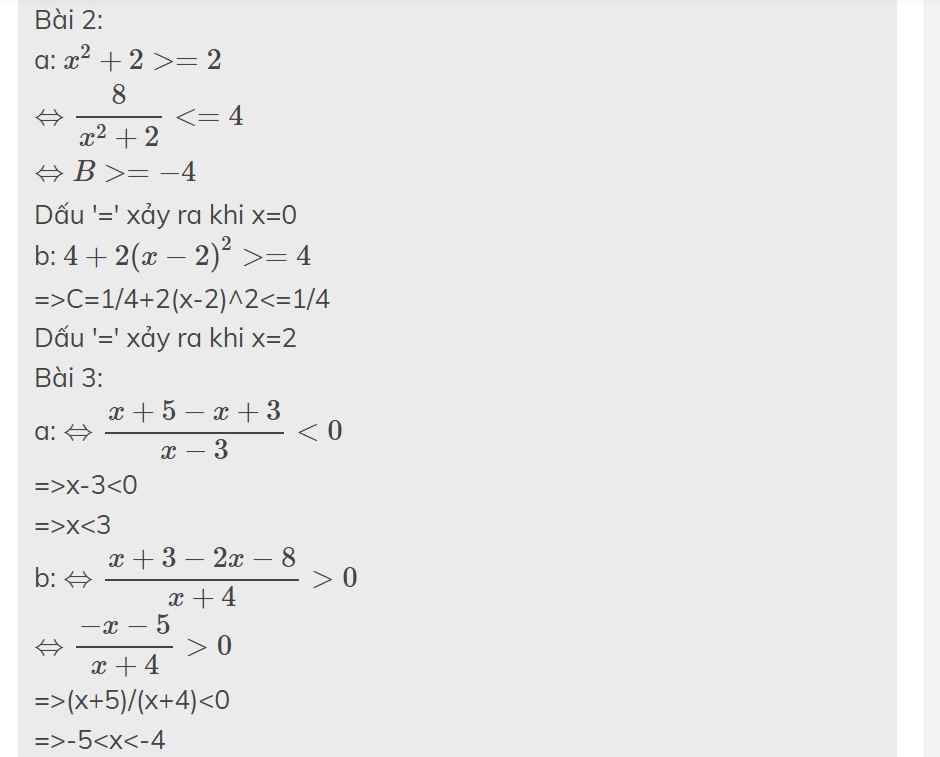
k mk đi
ai k mk
mk k lại
thanks