Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(2x^2+3\left(x+1\right)\left(x-1\right)-5x\left(x+1\right)\)
\(=2x^2+3\left(x^2-1\right)-5x^2-5x\)
\(=2x^2+3x^2-3-5x^2-5x\)
\(=\left(2x^2+3x^2-5x^2\right)-3-5x\)
\(=-\left(5x+3\right)\)
b, \(\left(4x+3y\right)\left(2x-5y\right)-\left(2x+6y\right)\left(3x-5y\right)\)
\(=8x^2-20xy+6xy-\left(15y^2-6x^2-10xy-18xy-30y^2\right)\)
\(=8x^2-20xy+6xy-15y^2+6x^2+10xy+18xy+30y^2\)
\(=\left(8x^2+6x^2\right)+\left(-20xy+6xy+10xy+18xy\right)+\left(-15y^2+30y^2\right)\)
\(=14x^2+14xy+15y^2\)
\(=14x.\left(x+y\right)+15y^2\)
Chúc bạn học tốt!!!

1) a) Đặt biểu thức là A
\(A=2x^2+4y^2-4xy-4x-4y+2017\)
\(A=\left(x-2y\right)^2+x^2-4x-4y+2017\)
\(A=\left(x-2y\right)^2+2\left(x-2y\right)+x^2-6x+2017\)
\(A=\left(x-2y-1\right)^2+\left(x+3\right)^2+2008\)
Vậy: MinA=2008 khi x=-3; y=-2
3) a) \(A=\dfrac{1}{x^2+x+1}\)
\(B=x^2+x+1=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
\(\Rightarrow B\ge\dfrac{3}{4}\Rightarrow A\ge\dfrac{4}{3}\)
Vậy MinA là \(\dfrac{4}{3}\) khi x=-0,5

1.
a) \(x\left(x+4\right)+x+4=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x+1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-4\\x=-1\end{matrix}\right.\)
b) \(x\left(x-3\right)+2x-6=0\)
\(\Leftrightarrow\left(x+2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\x-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\)
Bài 1:
a, \(x\left(x+4\right)+x+4=0\)
\(\Leftrightarrow x\left(x+4\right)+\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=-1\end{matrix}\right.\)
Vậy \(x=-4\) hoặc \(x=-1\)
b, \(x\left(x-3\right)+2x-6=0\)
\(\Leftrightarrow x\left(x-3\right)+2\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)
Vậy \(x=3\) hoặc \(x=-2\)

a) ĐKXĐ : \(x+y\ne0\)
\(x^2-2y^2=xy\)
\(x^2-y^2-y^2-xy=0\)
\(\left(x-y\right)\left(x+y\right)-y\left(y+x\right)=0\)
\(\left(x+y\right)\left(x-2y\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+y=0\left(Loai\right)\\x-2y=0\left(Chon\right)\end{matrix}\right.\)
Với x - 2y = 0 ta có x = 2y
Thay x = 2y vào A ta có :
\(A=\dfrac{2y-y}{2y+y}=\dfrac{y}{3y}=\dfrac{1}{3}\)

a) \(\dfrac{4x-1}{3x^2y}-\dfrac{7x-1}{3x^2y}\)
\(=\dfrac{\left(4x-1\right)-\left(7x-1\right)}{3x^2y}\)
\(=\dfrac{4x-1-7x+1}{3x^2y}\)
\(=\dfrac{-3x}{3x^2y}\)
\(=\dfrac{-1}{xy}\)
b) \(\dfrac{4x+5}{2x-1}-\dfrac{5-9x}{2x-1}\)
\(=\dfrac{\left(4x+5\right)-\left(5-9x\right)}{2x-1}\)
\(=\dfrac{4x+5-5+9x}{2x-1}\)
\(=\dfrac{13x}{2x-1}\)
c) \(\dfrac{11x}{2x-3}-\dfrac{x-18}{3-2x}\)
\(=\dfrac{11x}{2x-3}+\dfrac{x-18}{2x-3}\)
\(=\dfrac{11x+\left(x-18\right)}{2x-3}\)
\(=\dfrac{11x+x-18}{2x-3}\)
\(=\dfrac{12x-18}{2x-3}\)
\(=\dfrac{6\left(2x-3\right)}{2x-3}\)
\(=\dfrac{6}{1}\)
\(=6\)
d) \(\dfrac{2x-7}{10x-4}-\dfrac{3x+5}{4-10x}\)
\(=\dfrac{2x-7}{10x-4}+\dfrac{3x+5}{10x-4}\)
\(=\dfrac{\left(2x-7\right)+\left(3x+5\right)}{10x-4}\)
\(=\dfrac{2x-7+3x+5}{10x-4}\)
\(=\dfrac{5x-2}{10x-4}\)
\(=\dfrac{5x-2}{2\left(5x-2\right)}\)
\(=\dfrac{1}{2}\)

a)
\(\dfrac{x^3+2x^2-x-2}{x^3-3x+2}\)
\(=\dfrac{x^2\left(x+2\right)-\left(x+2\right)}{x^3-4x+x+2}\)
\(=\dfrac{\left(x+2\right)\left(x-1\right)\left(x+1\right)}{x\left(x^2-4\right)+\left(x+2\right)}\)
\(=\dfrac{\left(x+2\right)\left(x-1\right)\left(x+1\right)}{x\left(x-2\right)\left(x+2\right)+\left(x+2\right)}\)
\(=\dfrac{\left(x+2\right)\left(x-1\right)\left(x+1\right)}{\left(x+2\right)\left(x^2-2x+1\right)}\)
\(=\dfrac{\left(x+2\right)\left(x-1\right)\left(x+1\right)}{\left(x+2\right)\left(x-1\right)^2}\)
\(=\dfrac{x+1}{x-1}\)
b):
\(\dfrac{3x^2-7xy+4y^2}{2x^2+2xy-4y^2}\)
\(=\dfrac{3x^2-3xy-4xy+4y^2}{2x^2-2xy+4xy-4y^{ 2}}\)
\(=\dfrac{3x\left(x-y\right)-4y\left(x-y\right)}{2x\left(x-y\right)+4y\left(x-y\right)}\)
\(=\dfrac{\left(x-y\right)\left(3x-4y\right)}{\left(x-y\right) \left(2x+4y\right)}\)
\(=\dfrac{3x-4y}{2x+4y}\)
c):
\(\dfrac{x^2+5x}{2x+10}\)
\(=\dfrac{x\left(x+5\right)}{2\left(x+5\right)}\)
\(=\dfrac{x}{2}\)
\(\dfrac{x^3+2x^2-x-2}{x^3-3x+2}\)
= \(\dfrac{\left(x^3+2x^2\right)-\left(x+2\right)}{x^3-x-2x+2}\)
=\(\dfrac{x^2\left(x+2\right)-\left(x+2\right)}{\left(x^3-x\right)-\left(2x-2\right)}\)
= \(\dfrac{\left(x^2-1\right)\left(x+2\right)}{x\left(x^2-1\right)-2\left(x-1\right)}\)
= \(\dfrac{\left(x-1\right)\left(x+1\right)\left(x+2\right)}{x\left(x-1\right)\left(x+1\right)-2\left(x-1\right)}\)
= \(\dfrac{\left(x-1\right)\left(x+1\right)\left(x+2\right)}{\left(x-1\right)\left[x\left(x+1\right)-2\right]}\)
= \(\dfrac{\left(x-1\right)\left(x+1\right)\left(x+2\right)}{\left(x-1\right)\left(x^2+x-2\right)}\)
= \(\dfrac{\left(x-1\right)\left(x+1\right)\left(x+2\right)}{\left(x-1\right)\left(x^2-x+2x-2\right)}\)
= \(\dfrac{\left(x-1\right)\left(x+1\right)\left(x+2\right)}{\left(x-1\right)\left[\left(x^2-x\right)+\left(2x-2\right)\right]}\)
= \(\dfrac{\left(x-1\right)\left(x+1\right)\left(x+2\right)}{\left(x-1\right)\left[x\left(x-1\right)+2\left(x-1\right)\right]}\)
= \(\dfrac{\left(x-1\right)\left(x+1\right)\left(x+2\right)}{\left(x-1\right)\left(x-1\right)\left(x+2\right)}\)
= \(\dfrac{x+1}{x-1}\)
Mk thấy câu b) cứ sai sai kiểu j ý
c) \(\dfrac{x^2+5x}{2x+10}\)
= \(\dfrac{x\left(x+5\right)}{2\left(x+5\right)}\)
= \(\dfrac{x}{2}\)

Câu 3:
\(B=-3\left(x^2-\dfrac{1}{3}x-\dfrac{1}{3}\right)\)
\(=-3\left(x^2-2\cdot x\cdot\dfrac{1}{6}+\dfrac{1}{36}-\dfrac{13}{36}\right)\)
\(=-3\left(x-\dfrac{1}{6}\right)^2+\dfrac{13}{12}< =\dfrac{13}{12}\)
Dấu '=' xảy ra khi x=1/6
Bài 4:
\(C=\left(x+y\right)^2-4\left(x+y\right)+1\)
=3^2-4*3+1
=9+1-12
=-2


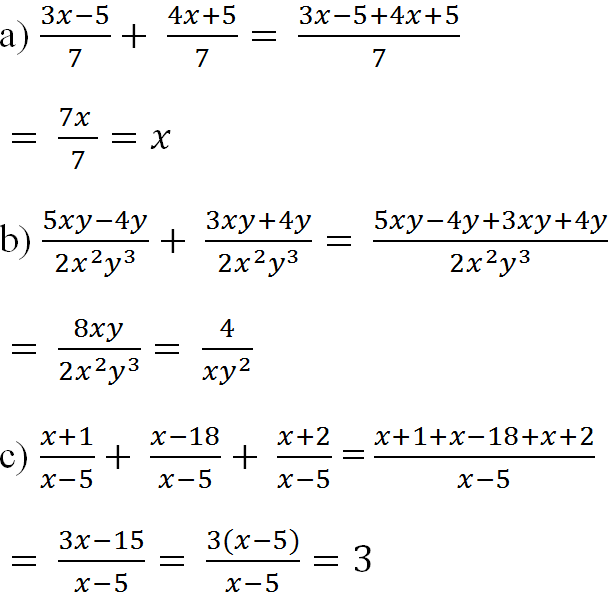
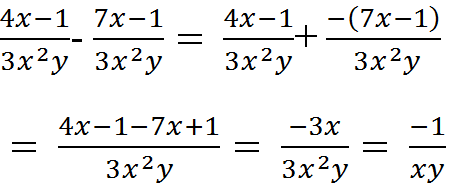
Ta có : 3x2 - 7xy + 4y2 = 0
=> 3x2 - 3xy - 4xy + 4y2 = 0
=> 3x( x - y) - 4y( x - y) = 0
=> ( x - y)( 3x - 4y) = 0
=> x = y ; 3x = 4y
Thay : x = y ; 3x = 4y vào phân thức trên ta có:
\(A=\dfrac{4y+2x}{5y-7x}+\dfrac{3x-2y}{10y-4x}\)
\(A=\dfrac{3x+2x}{5x-7x}+\dfrac{4y-2y}{10x-4x}\)
\(A=\dfrac{5x}{-2x}+\dfrac{2y}{6x}=\dfrac{5}{-2}+\dfrac{1}{3}=\dfrac{-13}{6}\)