Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)xét ΔABD và ΔAMD có:
góc BAD= góc MAD(AD là tia phân giác )
AD chung
góc ABD = góc AMD(=90độ) (ΔABC ⊥B; DM⊥AC)
⇒ΔABD=ΔAMD(ch-cgv)
b)Có:AB=AM (ΔABD=ΔAMD)
⇒A ϵ đường trung trực của BC (t/c đường trung trực)(1)
Lại có : BD=MD(ΔABD=ΔAMD)
⇒D ϵ đường trung trực BM(t/c đường trung trực) (2)
Từ (1) và(2)⇒AD là đường trung trực BM
c)Xét ΔBNDvàΔMCD có:
góc DBN =góc DMC (90độ)(ΔABC ⊥B; DM⊥AC)
BD=MD(ΔABD=ΔAMD)
góc BDN=MDC(2 góc dối đỉnh)
⇒ ΔBND=ΔMCD(g.c.g)
⇒BN=MC(2 cạnh tương ứng)
Có: AB+BN=AN và AM+MC=AC
Mà AB=AM(ΔABD=ΔAMD) và BN=MC (CMT)
⇒AN =AC
⇒ΔANC cân
Lại có góc A =60 độ
⇒ΔANC đều
A N B M I C D (Hình vẽ minh họa)
(hình vẽ minh họa)
d)CÓ: AD là tia phân giác góc BAC
⇒góc BAD= góc CAD=1/2 góc BAC=1/2 . 60độ=30 độ
⇒góc BAI=30độ
Lại có: góc NBD=90độ(ΔABC⊥B)
⇒BI<ND(quan hệ giữa góc và cạnh đối diện)

Xét ΔMAO và ΔNCO có
\(\widehat{MAO}=\widehat{NCO}\)
OA=OC
\(\widehat{MOA}=\widehat{NOC}\)
Do đó: ΔMAO=ΔNCO
Suy ra: MO=NO
hay O là trung điểm của MN

Bài 2:
a: Xét tứ giác DEBF có
BE//DF
BE=DF
Do đó: DEBF là hình bình hành
b: ta có: DEBF là hình bình hành
nên Hai đường chéo DB và EF cắt nhau tại trung điểm của mỗi đường(1)
Ta có:ABCD là hình bình hành
nên hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra BD,EF,AC đồng quy

a: Để (d)//(d1) thì \(\left\{{}\begin{matrix}m+1=-\dfrac{1}{2}\\-5< >3\left(đúng\right)\end{matrix}\right.\)
=>\(m+1=-\dfrac{1}{2}\)
=>\(m=-\dfrac{3}{2}\)
b: Thay x=2 vào y=x+3, ta được:
\(y=2+3=5\)
Thay x=2 và y=5 vào (d), ta được:
\(2\left(m+1\right)-5=5\)
=>2(m+1)=10
=>m+1=5
=>m=5-1=4
c: Tọa độ A là:
\(\left\{{}\begin{matrix}x=0\\y=\left(m+1\right)x-5=0\cdot\left(m+1\right)-5=-5\end{matrix}\right.\)
=>A(0;-5)
\(OA=\sqrt{\left(0-0\right)^2+\left(-5-0\right)^2}=\sqrt{0^2+5^2}=5\)
Tọa độ B là:
\(\left\{{}\begin{matrix}\left(m+1\right)x-5=0\\y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(m+1\right)x=5\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{m+1}\\y=0\end{matrix}\right.\)
=>\(B\left(\dfrac{5}{m+1};0\right)\)
\(OB=\sqrt{\left(\dfrac{5}{m+1}-0\right)^2+\left(0-0\right)^2}\)
\(=\sqrt{\left(\dfrac{5}{m+1}\right)^2}=\dfrac{5}{\left|m+1\right|}\)
Ox\(\perp\)Oy
=>OA\(\perp\)OB
=>ΔOAB vuông tại O
ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot5\cdot\dfrac{5}{\left|m+1\right|}=\dfrac{25}{2\left|m+1\right|}\)
Để \(S_{AOB}=5\) thì \(\dfrac{25}{2\left|m+1\right|}=5\)
=>\(2\left|m+1\right|=5\)
=>|m+1|=5/2
=>\(\left[{}\begin{matrix}m+1=\dfrac{5}{2}\\m+1=-\dfrac{5}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3}{2}\\m=-\dfrac{7}{2}\end{matrix}\right.\)
a: Vì \(2\ne1\) nên (d1) cắt (d2)
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}2x+1=x+1\\y=x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-x=1-1\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0+1=1\end{matrix}\right.\)
Vậy: (d1) giao (d2) tại M(0;1)
c: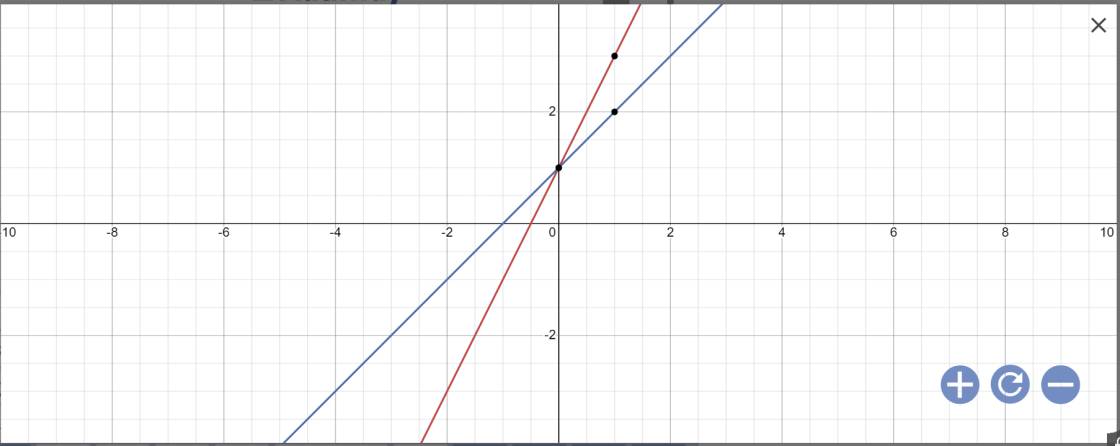
d: Gọi A,B lần lượt là giao điểm của (d1),(d2) với trục Ox
Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-\dfrac{1}{2}\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-1\end{matrix}\right.\)
Vậy: M(0;1); A(-0,5;0); B(-1;0)
\(MA=\sqrt{\left(-0,5-0\right)^2+\left(0-1\right)^2}=\dfrac{\sqrt{5}}{2}\)
\(MB=\sqrt{\left(-1-0\right)^2+\left(0-1\right)^2}=\sqrt{2}\)
\(AB=\sqrt{\left(-1+0,5\right)^2+\left(0-0\right)^2}=0,5\)
Xét ΔMAB có \(cosAMB=\dfrac{MA^2+MB^2-AB^2}{2\cdot MA\cdot MV}=\dfrac{\dfrac{5}{4}+2-0,25}{2\cdot\dfrac{\sqrt{5}}{2}\cdot\sqrt{2}}=\dfrac{3}{\sqrt{10}}\)
=>\(sinAMB=\sqrt{1-\left(\dfrac{3}{\sqrt{10}}\right)^2}=\dfrac{1}{\sqrt{10}}\)
Diện tích tam giác AMB là:
\(S_{AMB}=\dfrac{1}{2}\cdot MA\cdot MB\cdot sinAMB\)
\(=\dfrac{1}{2}\cdot\dfrac{1}{\sqrt{10}}\cdot\dfrac{\sqrt{5}}{2}\cdot\sqrt{2}=\dfrac{1}{4}\)
Giúp mình đi mn