Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)^2=9\\ \Leftrightarrow a+b+c+2\sqrt{ab}+2\sqrt{bc}+2\sqrt{ac}=9\\ \Leftrightarrow\sqrt{ab}+\sqrt{bc}+\sqrt{ac}=2\)
\(\Rightarrow\dfrac{\sqrt{a}}{a+2}+\dfrac{\sqrt{b}}{b+2}+\dfrac{\sqrt{c}}{c+2}=\dfrac{\sqrt{a}}{a+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}}+\dfrac{\sqrt{b}}{b+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}}+\dfrac{\sqrt{c}}{c+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}}\\ =\dfrac{\sqrt{a}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{c}\right)}+\dfrac{\sqrt{b}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{b}+\sqrt{c}\right)}+\dfrac{\sqrt{c}}{\left(\sqrt{b}+\sqrt{c}\right)\left(\sqrt{a}+\sqrt{c}\right)}\\ =\dfrac{\sqrt{a}\left(\sqrt{b}+\sqrt{c}\right)+\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)+\sqrt{c}\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{b}+\sqrt{c}\right)\left(\sqrt{a}+\sqrt{c}\right)}\\ =\dfrac{2\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{b}+\sqrt{c}\right)\left(\sqrt{a}+\sqrt{c}\right)}\\ =\dfrac{4}{\sqrt{\left(\sqrt{a}+\sqrt{b}\right)^2\left(\sqrt{b}+\sqrt{c}\right)^2\left(\sqrt{a}+\sqrt{c}\right)^2}}\)\(=\dfrac{4}{\sqrt{\left(a+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)\left(b+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)\left(c+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)}}\\ =\dfrac{4}{\sqrt{\left(a+2\right)\left(b+2\right)\left(c+2\right)}}\)

b: \(=\left(\sqrt{ab}+\dfrac{2\sqrt{ab}}{a}-\sqrt{\dfrac{a^2+1}{ab}}\right)\cdot\sqrt{ab}\)
\(=ab+\dfrac{2ab}{a}-\sqrt{a^2+1}=ab+2b-\sqrt{a^2+1}\)
c: \(=2\sqrt{6b}-6\sqrt{18}+10\sqrt{12}-\sqrt{48}\)
\(=2\sqrt{6b}-18\sqrt{2}+20\sqrt{3}-4\sqrt{3}\)
\(=2\sqrt{6n}-18\sqrt{2}+16\sqrt{3}\)
d: \(=\dfrac{\sqrt{3}\left(\sqrt{5}-\sqrt{2}\right)}{\sqrt{7}\left(\sqrt{5}-\sqrt{2}\right)}=\dfrac{\sqrt{21}}{7}\)

(bài 1) a) \(\dfrac{1}{5+2\sqrt{6}}-\dfrac{1}{5-2\sqrt{6}}\) = \(\dfrac{5-2\sqrt{6}-5-2\sqrt{6}}{25-24}\)
= \(\dfrac{-4\sqrt{6}}{1}\) = \(-4\sqrt{6}\)
b) \(\sqrt{6+2\sqrt{5}}-\dfrac{\sqrt{15}-\sqrt{3}}{\sqrt{3}}\) = \(\sqrt{\left(\sqrt{5}+1\right)^2}-\dfrac{\sqrt{3}\left(\sqrt{5}-1\right)}{\sqrt{3}}\)
= \(\left(\sqrt{5}+1\right)-\left(\sqrt{5}-1\right)\) = \(\sqrt{5}+1-\sqrt{5}+1\) = \(2\)
c) \(\dfrac{3\sqrt{2}-2\sqrt{3}}{\sqrt{3}-\sqrt{2}}:\dfrac{1}{\sqrt{16}}\) = \(\dfrac{\sqrt{6}\left(\sqrt{3}-\sqrt{2}\right)}{\sqrt{3}-\sqrt{2}}:\dfrac{1}{\sqrt{16}}\)
= \(\sqrt{6}.\sqrt{16}\) = \(4\sqrt{6}\)
d) \(\dfrac{3+2\sqrt{3}}{\sqrt{3}}+\dfrac{2+\sqrt{2}}{1+\sqrt{2}}-\dfrac{1}{2-\sqrt{3}}\)
= \(\dfrac{\sqrt{3}\left(\sqrt{3}+2\right)}{\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{1+\sqrt{2}}-\dfrac{1}{2-\sqrt{3}}\)
= \(\sqrt{3}+2+\sqrt{2}-\dfrac{1}{2-\sqrt{3}}\) = \(\dfrac{\left(\sqrt{3}+2+\sqrt{2}\right)\left(2-\sqrt{3}\right)-1}{2-\sqrt{3}}\)
= \(\dfrac{2\sqrt{3}-3+4-2\sqrt{3}+2\sqrt{2}-\sqrt{6}-1}{2-\sqrt{3}}\)
= \(\dfrac{2\sqrt{2}-\sqrt{6}}{2-\sqrt{3}}\) = \(\dfrac{\sqrt{2}\left(2-\sqrt{3}\right)}{2-\sqrt{2}}\) = \(\sqrt{2}\)
e) \(\dfrac{4}{1+\sqrt{3}}-\dfrac{\sqrt{15}+\sqrt{3}}{1+\sqrt{5}}\) = \(\dfrac{4}{1+\sqrt{3}}-\dfrac{\sqrt{3}\left(\sqrt{5}+1\right)}{1+\sqrt{5}}\)
= \(\dfrac{4}{1+\sqrt{3}}-\sqrt{3}\) = \(\dfrac{4-\sqrt{3}-3}{1+\sqrt{3}}\) = \(\dfrac{1-\sqrt{3}}{1+\sqrt{3}}\)
= \(\dfrac{\left(1-\sqrt{3}\right)\left(1-\sqrt{3}\right)}{1-3}\) = \(\dfrac{1-2\sqrt{3}+3}{-2}\) = \(\dfrac{4-2\sqrt{3}}{-2}\)
= \(\dfrac{-2\left(-2+\sqrt{3}\right)}{-2}\) = \(\sqrt{3}-2\)
bài 2)
a)\(\dfrac{a+b-2\sqrt{ab}}{\sqrt{a}-\sqrt{b}}:\dfrac{1}{\sqrt{a}+\sqrt{b}}=\dfrac{\left(a+b-2\sqrt{ab}\right)\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\)
= \(\dfrac{a\sqrt{a}+a\sqrt{b}+b\sqrt{a}+b\sqrt{b}-2a\sqrt{b}-2b\sqrt{a}}{\sqrt{a}-\sqrt{b}}\)
= \(\dfrac{a\sqrt{a}+-a\sqrt{b}+b\sqrt{b}-b\sqrt{a}}{\sqrt{a}-\sqrt{b}}\) = \(\dfrac{a\left(\sqrt{a}-\sqrt{b}\right)-b\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\)
= \(\dfrac{\left(a-b\right)\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\) = \(a-b\)
b) \(\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right).\left(\dfrac{a-\sqrt{a}}{\sqrt{a}+1}-\dfrac{a+\sqrt{a}}{\sqrt{a}-1}\right)\)
= \(\dfrac{2a-2}{4\sqrt{a}}.\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)^2-\sqrt{a}\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
= \(\dfrac{2a-2}{4\sqrt{a}}.\dfrac{\sqrt{a}\left(a-2\sqrt{a}+1\right)-\sqrt{a}\left(a+2\sqrt{a}+1\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
= \(\dfrac{2a-2}{4\sqrt{a}}.\dfrac{a\sqrt{a}-2a+\sqrt{a}-a\sqrt{a}-2a-\sqrt{a}}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
= \(\dfrac{2\left(a-1\right)}{4\sqrt{a}}.\dfrac{-4a}{a-1}\) = \(-2\)

Câu 1 :
a ) \(\sqrt{0,36.100}=\sqrt{36}=6\)
b ) \(\sqrt[3]{-0,008}=\sqrt[3]{\left(-0,2\right)^3}=-0,2\)
c ) \(\sqrt{12}+6\sqrt{3}+\sqrt{27}=2\sqrt{3}+6\sqrt{3}+3\sqrt{3}=11\sqrt{3}\)
Câu 2 :
a ) \(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{a}+\sqrt{b}}=\dfrac{\left(\sqrt{a}+\sqrt{b}\right)\left(a-\sqrt{ab}+b\right)}{\sqrt{a}+\sqrt{b}}=a-\sqrt{ab}+b\)

Bài 1 bạn nhóm , trục như thường nhé :D
Bài 2. \(a.A=\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}=\sqrt{3+2\sqrt{3}.\sqrt{2}+2}-\sqrt{3-2\sqrt{3}.\sqrt{2}+2}=\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}=2\sqrt{2}\)
\(b.B=\sqrt{17-12\sqrt{2}}-\sqrt{9+4\sqrt{2}}=\sqrt{9-2.2\sqrt{2}.3+8}-\sqrt{8+2.2\sqrt{2}+1}=3-2\sqrt{2}-2\sqrt{2}-1=2-4\sqrt{2}\)
\(c.C=\sqrt{13+30\sqrt{2+\sqrt{9+4\sqrt{2}}}}=\sqrt{13+30\sqrt{2+\sqrt{8+2.2.\sqrt{2}+1}}}=\sqrt{13+30\sqrt{2+2\sqrt{2}+1}}=\sqrt{43+30\sqrt{2}}=\sqrt{25+2.3\sqrt{2}.5+18}=5+3\sqrt{2}\)
\(d.D=\sqrt{12-3\sqrt{7}}-\sqrt{12+3\sqrt{7}}\)
\(D^2=24-2\sqrt{\left(12-3\sqrt{7}\right)\left(12+3\sqrt{7}\right)}=24-2\sqrt{81}=24-18=6\)
\(D=-\sqrt{6}\left(do:D< 0\right)\)

Câu 2:
a: \(=2\left(\sqrt{4+\sqrt{5}-1}\right)\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\sqrt{2}\cdot\sqrt{6+2\sqrt{5}}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=2\cdot\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)=8\)
b: \(=\dfrac{a-2\sqrt{a}+1+a+2\sqrt{a}+1}{a-1}\cdot\left(\dfrac{a+1-2}{a+1}\right)^2\)
\(=\dfrac{2\left(a+1\right)}{a-1}\cdot\dfrac{\left(a-1\right)^2}{\left(a+1\right)^2}=\dfrac{2\left(a-1\right)}{a+1}\)

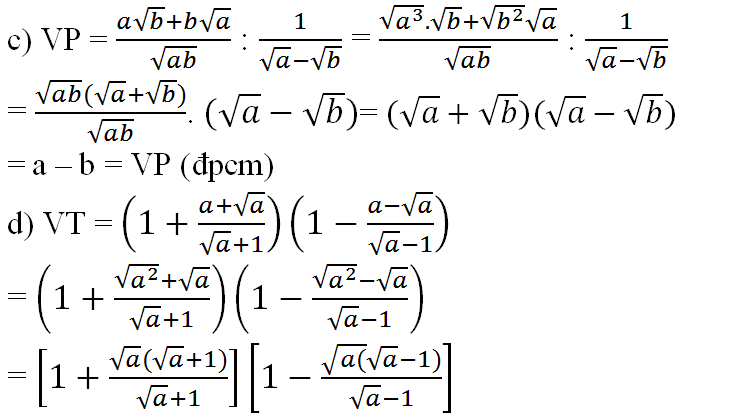




\(P=\dfrac{\left(5+2\sqrt{6}\right)\sqrt{5-2\sqrt{6}}}{\sqrt{3}+\sqrt{2}}\)
=\(\dfrac{\left(3+2\sqrt{2.3}+2\right)\sqrt{3-2\sqrt{3.2}+2}}{\sqrt{3}+\sqrt{2}}\)
=\(\dfrac{\left(\sqrt{3}+\sqrt{2}\right)^2\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}}{\sqrt{3}+\sqrt{2}}\)
=\(\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{3}-\sqrt{2}\right)\)
=\(3-2=1\)
ta có : \(\dfrac{1}{\sqrt{a}+\sqrt{b}}+\dfrac{1}{\sqrt{b}+\sqrt{c}}\ge2\sqrt{\dfrac{1}{\sqrt{ab}+\sqrt{ac}+\sqrt{bc}+b}}\)
\(\ge\dfrac{2}{\sqrt{a+b+c+b}}=\dfrac{2}{\sqrt{4b}}=\dfrac{2}{2\sqrt{b}}=\dfrac{1}{\sqrt{b}}=\dfrac{2}{\sqrt{a+c}}\ge\dfrac{2}{\sqrt{a}+\sqrt{b}}\)
dấu "=" xảy ra khi \(a=b=c\Leftrightarrow a+c=2b\Rightarrow\left(đpcm\right)\)