Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng bđt \(\frac{x^2}{m}+\frac{y^2}{n}+\frac{z^2}{p}\ge\frac{\left(x+y+z\right)^2}{m+n+p}\) ta có
\(\frac{a^3}{b}+\frac{b^3}{c}+\frac{c^3}{a}=\frac{a^4}{ab}+\frac{b^4}{bc}+\frac{c^4}{ac}\ge\frac{\left(a^2+b^2+c^2\right)^2}{ab+bc+ac}\ge\frac{\left(a^2+b^2+c^2\right)^2}{a^2+b^2+c^2}=a^2+b^2+c^2\)
Bài 1. Đặt \(a=\sqrt{x+3},b=\sqrt{x+7}\)
\(\Rightarrow a.b+6=3a+2b\) và \(b^2-a^2=4\)
Từ đó tính được a và b
Bài 2. \(\frac{2x-1}{x^2}+\frac{y-1}{y^2}+\frac{6z-9}{z^2}=\frac{9}{4}\)
\(\Leftrightarrow\frac{2}{x}-\frac{1}{x^2}+\frac{1}{y}-\frac{1}{y^2}+\frac{6}{z}-\frac{9}{z^2}-\frac{9}{4}=0\)
Đặt \(a=\frac{1}{x},b=\frac{1}{y},c=\frac{1}{z}\)
Ta có \(2a-a^2+b-b^2+6c-9c^2-\frac{9}{4}=0\)
\(\Leftrightarrow-\left(a^2-2a+1\right)-\left(b^2-b+\frac{1}{4}\right)-\left(9c^2-6c+1\right)=0\)
\(\Leftrightarrow-\left(a-1\right)^2-\left(b-\frac{1}{2}\right)^2-\left(3c-1\right)^2=0\)
Áp dụng tính chất bất đẳng thức suy ra a = 1 , b = 1/2 , c = 1/3
Rồi từ đó tìm được x,y,z

a) Vì a,b không âm nên căn có nghĩa.
Ta có: \(\sqrt{a}\) = \(a^2\) ; \(\sqrt{b}\) = \(b^2\)
Vì a < b nên \(a^2\) < \(b^2\)
=> \(\sqrt{a}\) < \(\sqrt{b}\) (dpcm)
b) Vì a, b không âm nên căn có nghĩa.
Ta có: \(\sqrt{a}\) < \(\sqrt{b}\) => \(\left(\sqrt{a}\right)^2\) < \(\left(\sqrt{b}\right)^2\) => a < b (dpcm)

a) \(P=\left(\frac{\sqrt{x}}{\sqrt{x}-2}+\frac{1}{\sqrt{x}+2}-\frac{2}{4-x}\right):\frac{\sqrt{x}+3}{\sqrt{x}-2}\left(ĐK:x\ge0;x\ne4\right)\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+2\right)+\sqrt{x}-2+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\frac{\sqrt{x}-2}{\sqrt{x}+3}\)
\(=\frac{x+2\sqrt{x}+\sqrt{x}}{\sqrt{x}+2}\cdot\frac{1}{\sqrt{x}+3}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+3\right)}{\sqrt{x}+2}\cdot\frac{1}{\sqrt{x}+3}=\frac{\sqrt{x}}{\sqrt{x}+2}\)
b) Vì: \(\sqrt{x}+4>0,\forall x\inĐK\)
=> \(2\sqrt{x}+4>\sqrt{x}\)
=> \(\frac{\sqrt{x}}{2\sqrt{x}+4}< 0\)
=> \(\frac{\sqrt{x}}{\sqrt{x}+2}< 2\)
=>đpcm

Ta có:
\(x^4+4=\left(x^4+4x^2+4\right)-4x^2\)
=\(\left(x^2+2\right)^2-\left(2x\right)^2=\left(x^2+2x+2\right)\left(x^2-2x+2\right)\)
=> \(x^4+4\) chia hết cho \(x^2+2x+a\) khi \(\left(x^2+2x+2\right)\left(x^2-2x+2\right)⋮\left(x^2+2x+a\right)\)
=> a = 2.
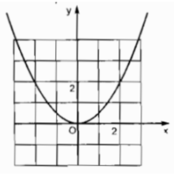
 Giải thích dùm mình sao
Giải thích dùm mình sao 
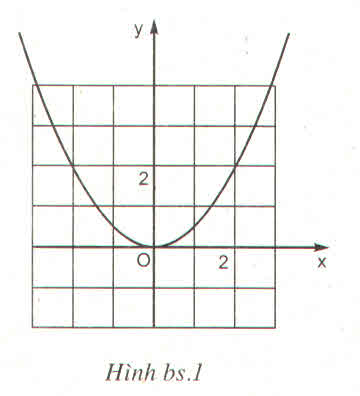



Dựa vào đồ thị hàm số ta thấy đồ thị hàm số đi qua điểm (2;2)
Do đó, tọa độ điểm (2;2) thỏa mãn phương trình hàm số:
Chọn đáp án D