Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(P) có đỉnh là I(-1;5) => \(-\frac{b}{2a}=-1\Rightarrow b=2a\) (1)
và (P) đi qua I(-1; 5) => tại x = -1; y = 5 thì a - b + c = 5 (2)
(P) đi qua điểm A(1; 1) => tại x = 1; y = 1 thì a + b + c = 1(3)
thế (1) vào (2): -a + c = 5
thế (1) vào (3): 3a + c = 1
giải hệ phtrinh ta được a = -1; c = 4
=> b = 2a = -2
giá trị biểu thức 3a + 2b + c = -3 - 4 + 4 = -3

4A
5. \(\left\{{}\begin{matrix}a+b+2=5\\4a-2b+2=8\end{matrix}\right.\) \(\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\) \(\Rightarrow y=2x^2+x+2\)
6. \(\left\{{}\begin{matrix}-\frac{b}{2a}=-2\\\frac{4ac-b^2}{4a}=4\\c=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=4a\\24a-16a^2=16a\\c=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\frac{1}{2}\\b=2\\c=6\end{matrix}\right.\) \(\Rightarrow y=\frac{1}{2}x^2+2x+6\)
7. \(\left\{{}\begin{matrix}c=-1\\a+b+c=-1\\a-b+c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-1\\c=-1\end{matrix}\right.\) \(\Rightarrow y=x^2-x-1\)
8.
a/ \(AM=\sqrt{2}\)
b/ \(AM=\sqrt{10}\)
c/ Không thuộc đồ thị
d/ Không thuộc đồ thị
Đáp án A đúng

Từ đề bài ta có:
a/ \(\left\{{}\begin{matrix}0.a+0.b+c=0\\a+b+c=1\\a-b+c=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-1\\b=2\\c=0\end{matrix}\right.\) \(\Rightarrow y=-x^2+2x\)
b/ \(\left\{{}\begin{matrix}a+b+c=0\\4a+2b+c=8\\0.a+0.b+c=-6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=5\\c=-6\end{matrix}\right.\)
c/ \(\left\{{}\begin{matrix}0.a+0.b+c=5\\-\frac{b}{2a}=3\\\frac{b^2-4ac}{4a}=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-6\\c=5\end{matrix}\right.\)
d/ \(\left\{{}\begin{matrix}a+b+c=0\\4a+2b+c=0\\-\frac{b}{2a}=\frac{3}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=k\\b=-3k\\c=2k\end{matrix}\right.\) với k là số thực khác 0 bất kì

Từ đề bài \(\Rightarrow a>0\) và:
\(\left\{{}\begin{matrix}\frac{4ac-b^2}{4a}=-5\\a+b+c=-1\\c=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b^2=36a\\a+b=-5\\c=4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=\frac{b^2}{36}\\\frac{b^2}{36}+b+5=0\\c=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-6\\c=4\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}a=25\\b=-30\\c=4\end{matrix}\right.\)

a) Vì parabol đi qua M(1; 5) nên tọa độ của M nghiệm đúng phương trình của parabol: 5 = a.12 + b.1 + 2.
Tương tự, với N(- 2; 8) ta có: 8 = a.(- 2)2 + b.(- 2) + 2
Giải hệ phương trình: ta được a = 2, b = 1.
Parabol có phương trình là: y = 2x2 + x + 2.
b) Giải hệ phương trình:
Parabol: y = x2 - x + 2.
c) Giải hệ phương trình:
Parabol: y = x2 - 4x + 2.
d) Ta có:
Parabol: y = 16x2 + 12x + 2 hoặc y = x2 - 3x + 2.

Tìm Parabol (P): y=ax2+bx+c đi qua điểm A(1;0) và có tung độ đỉnh bằng -1
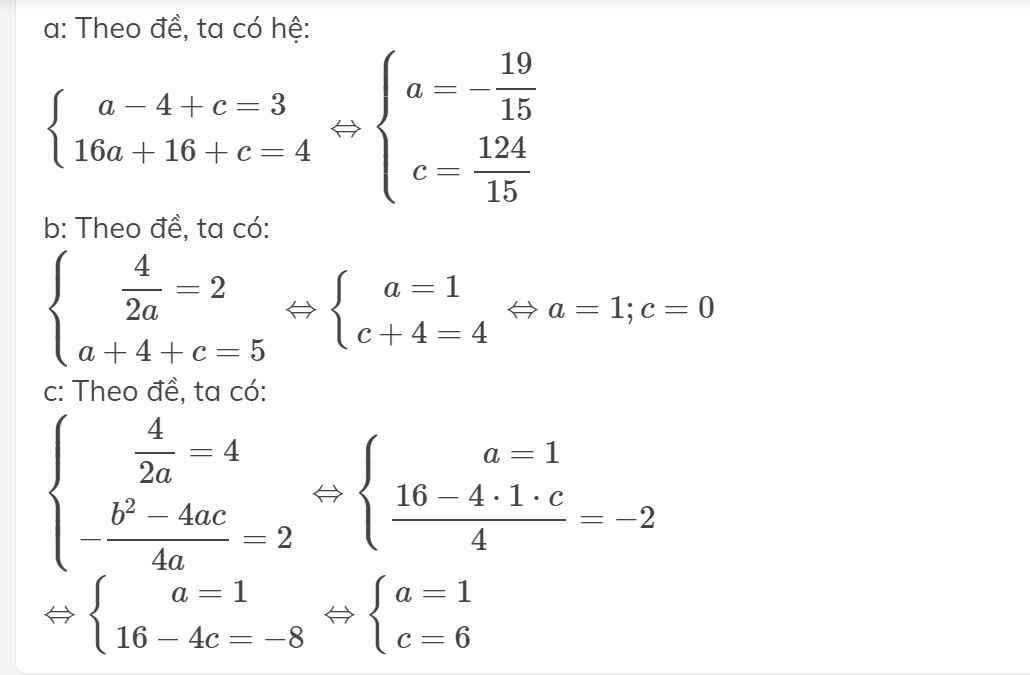
Theo mk thì cứ thay vào r ghpt
Vì \(M\left(1;5\right)\in\left(P\right)\)
Thay x=1;y=5
\(a+b+2=5\Leftrightarrow a+b=3\)
tương tự
\(4a-2b+2=8\Leftrightarrow4a-2b=6\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=3\\4a-2b=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\)
\(\Rightarrow a+2b=2+2=4\)