Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là số luống rau, y là số cây của mỗi luống.
(Điều kiện x > 0, y > 0)
+ Tăng 8 luống, mỗi luống ít hơn 3 cây thì số cây toàn vườn ít đi 54 cây, ta được: (x + 8)(y – 3) = xy – 54
+ Giảm 4 luống mỗi luống tăng thêm 2 cây thì số cây toàn vườn tăng 32 cây, nên ta được: (x – 4)(y + 2) = xy + 32
+ Ta được hệ phương trình: 
Giải ra ta được: x = 50, y = 15
=> Số cây rau cải bắp nhà Lan trồng trong vường là:
50.15 = 750 (cây).

Gọi x là số luống rau , y là số rau mỗi luống
Điều kiện : x > 4 ; y > 3 ; \(x,y\in N\)
Số cây trong vườn là : xy ( cây )
+ Tăng 8 luống , mỗi luống ít hơn 3 cây thì số luống là x + 8 , số cây mỗi luống là y - 3
=> Tổng số cây trong vườn là : ( x + 8 )( y - 3 ) cây
Số cây trong vườn ít hơn 54 cây nên ta có p/trình :
\(\left(x+8\right)\left(y-3\right)=xy-54\)
\(\Leftrightarrow xy-3x+8y-24=xy-54\)
\(\Leftrightarrow xy-3x+8y-xy=-54+24\)
\(\Leftrightarrow-3x+8y=-30\)
\(\Leftrightarrow3x-8y=30\)
+ Giảm 4 luống mỗi luống tăng thêm 2 cây thì số luống là x – 4 và số cây mỗi luống là y + 2
=> Số cây trong vườn là: (x – 4)(y + 2) cây
Số cây trong vườn tăng thêm 32 cây nên ta có phương trình :
(x – 4)(y + 2) = xy + 32
<=> xy – 4y + 2x – 8 = xy + 32
<=> 2x – 4y = 40
Ta có hệ phương trình :
\(\hept{\begin{cases}3x-8y=30\\2x-4y=40\end{cases}\Leftrightarrow\hept{\begin{cases}3x-8y=30\\4x-8y=80\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}4x-8y-\left(3x-8y\right)=50\\4x-8y=80\end{cases}\Leftrightarrow}\hept{\begin{cases}x=50\\y=15\end{cases}\left(tmđk\right)}\)
Vậy số rau cải bắp nhà Lan trồng là : 15 . 50 = 750 cây

Gọi x là số luống rau, y là số cây mỗi luống.
Điều kiện x > 4, y > 3; x,y ∈ N
Số cây trong vườn là: x.y (cây)
+ Tăng 8 luống, mỗi luống ít hơn 3 cây thì số luống là x + 8, số cây mỗi luống là y – 3
⇒ Tổng số cây trong vườn là (x + 8)(y – 3) cây.
Số cây trong vườn ít đi 54 cây nên ta có phương trình:
(x + 8)(y – 3) = xy – 54
⇔ xy -3x + 8y -24 = xy – 54
⇔ 3x – 8y = 30
+ Giảm 4 luống mỗi luống tăng thêm 2 cây thì số luống là x – 4 và số cây mỗi luống là y + 2.
⇒ Số cây trong vườn là: (x – 4)(y + 2) cây
Số cây trong vườn tăng thêm 32 cây nên ta có phương trình:
(x – 4)(y + 2) = xy + 32
⇔ xy – 4y + 2x – 8 = xy + 32
⇔ 2x – 4y = 40
Ta có hệ phương trình:
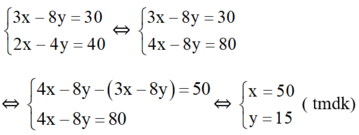
Vậy số rau cải bắp nhà Lan trồng là : 15.50 = 750 cây.

Gọi x là số luống rau, y là số cây mỗi luống.
Điều kiện x > 4, y > 3; x,y ∈ N
Số cây trong vườn là: x.y (cây)
+ Tăng 8 luống, mỗi luống ít hơn 3 cây thì số luống là x + 8, số cây mỗi luống là y – 3
⇒ Tổng số cây trong vườn là (x + 8)(y – 3) cây.
Số cây trong vườn ít đi 54 cây nên ta có phương trình:
(x + 8)(y – 3) = xy – 54
⇔ xy -3x + 8y - 24 = xy – 54
⇔ xy -3x + 8y - xy = –54 + 24
⇔ -3x + 8y = –30
⇔ 3x – 8y = 30
+ Giảm 4 luống mỗi luống tăng thêm 2 cây thì số luống là x – 4 và số cây mỗi luống là y + 2.
⇒ Số cây trong vườn là: (x – 4)(y + 2) cây
Số cây trong vườn tăng thêm 32 cây nên ta có phương trình:
(x – 4)(y + 2) = xy + 32
⇔ xy – 4y + 2x – 8 = xy + 32
⇔ 2x – 4y = 40
Ta có hệ phương trình:
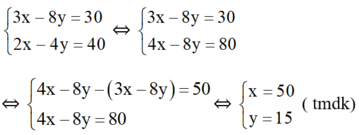
Vậy số rau cải bắp nhà Lan trồng là : 15.50 = 750 cây.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình:
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.

Gọi chiều dài là a (a khác 0) (m)
chiều rộng là a - 4 (m)
Diện tích là a . (a - 4) (m2)
Mà diện tích mảnh vườn bằng 320 m2 nên ta có pt:
a . (a - 4) = 320
Giải pt => a = 20
chiều dài là 20 m; chiều rộng là 16 m.

Gọi chiều dài mảnh vườn là: `x (m)` `ĐK: x > 0`
`=>` Chiều rộng mảnh vườn là: `x-5 (m)`
`=>` Diện tích mảnh vườn là: `x (x-5) (m^2)`
Vì nếu tăng chiều rộng gấp đôi thì diện tích mảnh vườn tăng `300 m^2` nên ta có ptr:
`2(x-5).x=x(x-5)+300`
`<=>2x^2-10x=x^2-5x+300`
`<=>x^2-5x-300=0`
`<=>x^2-20x+15x-300=0`
`<=>(x-20)(x+15)=0`
`<=>` $\left[\begin{matrix} x=20(t/m)\\ x=-15(ko t/m)\end{matrix}\right.$
Vậy chiều dài mảnh vườn là `20 m`, chiều rộng là `20-5=15 m`

Diện tích mảnh vườn là:
\(1200000:20000=60\left(m^2\right)\)
Gọi chiều rộng mảnh vườn là x (m) với x>0
Chiều dài mảnh vườn là: \(x+4\) (m)
Diện tích mảnh vườn là: \(x\left(x+4\right)\) \(\left(m^2\right)\)
Do diện tích mảnh vườn là 60 \(m^2\) nên ta có pt:
\(x\left(x+4\right)=60\)
\(\Leftrightarrow x^2+4x-60=0\Rightarrow\left[{}\begin{matrix}x=6\\x=-10\left(loại\right)\end{matrix}\right.\)
Vậy mảnh vườn rộng 6m
Giải nhanh giúp mình với