Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{1991.1992.1993.1994.995}{1990.1991.1992.1993.997}=\frac{1994.995}{1990.997}=\frac{2.1}{2.1}=\frac{2}{2}=1\)

\(\frac{4}{1x3x5}+\frac{4}{3x5x7}+...+\frac{4}{9x11x13}\)
\(=\frac{1}{1x3}-\frac{1}{3x5}+\frac{1}{3x5}-...+\frac{1}{9x11}-\frac{1}{11x13}\)
\(=\frac{1}{3}-\frac{1}{143}\)
\(=\frac{140}{429}\)

\(\frac{4}{1.3.5}+\frac{4}{3.5.7}+\frac{4}{5.7.9}+\frac{4}{7.9.11}+\frac{4}{9.11.13}\)
= \(\frac{1}{1.3.5}+\frac{1}{3.5.7}+\frac{1}{5.7.9}+\frac{1}{7.9.11}+\frac{1}{9.11.13}\)
= \(\frac{1}{1.3}-\frac{1}{3.5}+\frac{1}{3.5}-\frac{1}{5.7}+...+\frac{1}{9.11}-\frac{1}{11.13}\)
= \(\frac{1}{1.3}-\frac{1}{11.13}\)
= \(\frac{140}{429}\)
~~~
Không chắc chắn lắm nhé :3
#Sunrise
nhớ cho k nhé !
4/1x3x5 = 1/1x3 - 1/3x5
4/3x5x7 = 1/3x5 - 1/5x7
.............
A = 1/1x3 - 1/11x13
1/1x3x5 = 1/4 x (1/1x3 - 1/3x5)
1/3x5x7 = 1/4 x (1/3x5 - 1/5x7)
..........
B = 1/4 x (1/1x3 - 1/11x13)



Bài 1
a; \(\dfrac{7}{19}\) x \(\dfrac{1}{3}\) + \(\dfrac{7}{19}\) x \(\dfrac{2}{3}\)
= \(\dfrac{7}{19}\) x (\(\dfrac{1}{3}+\dfrac{2}{3}\))
= \(\dfrac{7}{19}\) x 1
= \(\dfrac{7}{19}\)
b; 15 x \(\dfrac{2121}{4343}\) + 15 x \(\dfrac{212121}{434343}\)
= 15 x \(\dfrac{21}{43}\) + 15 x \(\dfrac{21}{43}\)
= 15 x \(\dfrac{21}{43}\) x (1 + 1)
= 15 x \(\dfrac{21}{43}\) x 2
= (15 x 2) x \(\dfrac{21}{43}\)
= 30 x \(\dfrac{21}{43}\)
= \(\dfrac{630}{43}\)
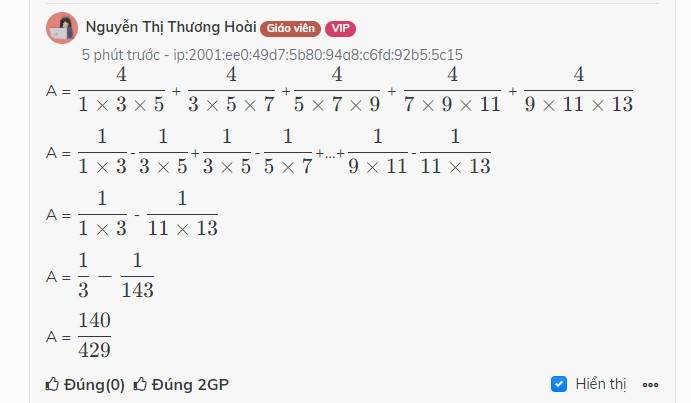
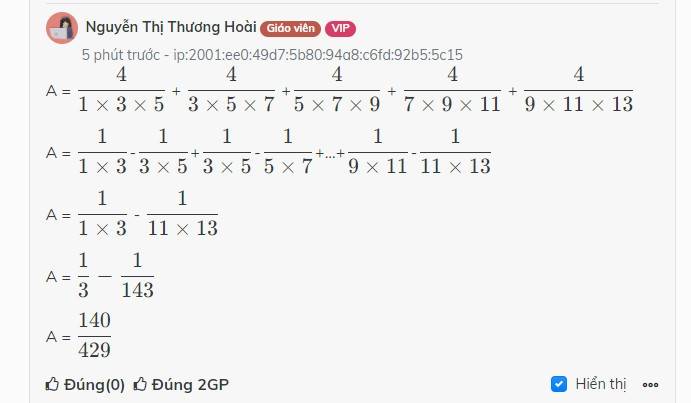
A = \(\dfrac{4}{1\times3\times5}\) + \(\dfrac{4}{3\times5\times7}\) +\(\dfrac{4}{5\times7\times9}\) + \(\dfrac{4}{7\times9\times11}\) + \(\dfrac{4}{9\times11\times13}\)
A = \(\dfrac{1}{1\times3}\)-\(\dfrac{1}{3\times5}\)+\(\dfrac{1}{3\times5}\)-\(\dfrac{1}{5\times7}\)+...+\(\dfrac{1}{9\times11}\)-\(\dfrac{1}{11\times13}\)
A = \(\dfrac{1}{1\times3}\) - \(\dfrac{1}{11\times13}\)
A = \(\dfrac{1}{3}-\dfrac{1}{143}\)
A = \(\dfrac{140}{429}\)
Bài 2:
A = \(\dfrac{1991}{1990}\) x \(\dfrac{1992}{1991}\) x \(\dfrac{1993}{1992}\) x \(\dfrac{1994}{1993}\) x \(\dfrac{1995}{997}\)
A = \(\dfrac{1994\times1995}{1990\times997}\)
A = \(\dfrac{997\times2\times5\times399}{5\times2\times199\times997}\)
A = \(\dfrac{399}{199}\)