DQ
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 10 2019
\(x^{2019}-y^{2019}+2\left(x-y\right)=0\)
<=> \(\left(x-y\right)\left(x^{2018}+x^{2017}y+...+xy^{2017}+y^{2018}\right)+2\left(x-y\right)=0\)
<=> \(\left(x-y\right)\left(x^{2018}+x^{2017}y+...+xy^{2017}+y^{2018}+2\right)=0\)(1)
Có: \(x^{2018}+x^{2017}y+...+xy^{2017}+y^{2018}+2>0\)mọi x, y.
(1) <=> \(x-y=0\)
<=> x = y
Thế vào P ta có:
\(P=x^4-2x^2+2=\left(x^2-1\right)^2+1\ge1\)
"=" xảy ra <=> \(y=x=\pm1\)
Vậy min P =1 khi và chỉ khi x = y =1 hoặc x = y =-1.
9 tháng 11 2017
đã hỏi thầy giáo và đã hiêu câu này. Quả thực đáp án A là đúng
Cảm ơn ai đang đã quan tâm đến.
13 tháng 11 2016
Đặt x=log9t (t>0), phương trình đã cho trở thành:
\(2^{3log_9t}+3^{2log_9t}=17\Leftrightarrow8^{log_9t}+t=17\)
Đặt \(f\left(t\right)=8^{log_9t}+t-17\)
ta thấy f(t) là hàm đồng biến trên khoảng \(\left(0;+\infty\right)\) mà f(9)=0
do đó t=9 là nghiệm duy nhất của phương trình f(t)=0
t=9 nên x=1
3 tháng 4 2019
đáp án:
Hàm số đã cho xác định trên D = R.
Với m = -1. Khi đó hàm số trở thành y = -2x + 4 ; y' = -2 < 0 ∀x∈R, không thỏa mãn yêu cầu bài toán.
Với m ≠ -1. Ta có f'(x)= 3(m+1)x2 - 6(m + 1)x + 2m
+ Hàm số đồng biến trên khoảng có độ dài không nhỏ hơn 1 khi và chỉ khi f'(x) = 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn [x1;x2 ] thỏa mãn |x1 - x2 | ≥ 1
+ f'(x)= 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn[x1;x2]
Theo Viét ta có 
+ Với |x1 - x2 | ≥ 1 ⇔ (x1 + x2 )2 - 4x1 x2 - 1 ≥ 0
Đối chiếu điều kiện ta có m ≤ -9.
29 tháng 7 2019
Có: \(z^2\ge2\left(x^2+y^2\right)\ge\left(x+y\right)^2\)\(\Leftrightarrow\)\(-z\le x+y\le z\)
And: \(\frac{z^2}{4}\ge\frac{x^2+y^2}{2}\ge\frac{2xy}{2}=xy\)
=> \(\frac{1}{x^4}+\frac{1}{y^4}+\frac{1}{z^4}\ge2\sqrt{\frac{1}{\left(xy\right)^4}}+\frac{1}{z^4}=\frac{2}{\left(xy\right)^2}+\frac{1}{z^4}\ge\frac{2}{\left(\frac{z^2}{4}\right)^2}+\frac{1}{z^4}=\frac{33}{z^4}\)
And: \(x^4+y^4+z^4\ge\frac{\left(x^2+y^2\right)^2}{2}+\frac{z^4}{4}+\frac{3z^4}{4}\ge\frac{\left(x^2+y^2+z^2\right)^2}{6}+\frac{3z^4}{4}\)
\(\ge\frac{\left(\frac{\left(x+y\right)^2}{2}+z^2\right)^2}{6}+\frac{3z^4}{4}\ge\frac{\left(\frac{\left(-z\right)^2}{2}+z^2\right)^2}{6}+\frac{3z^4}{4}=\frac{\frac{9z^4}{4}}{6}+\frac{3z^4}{4}=\frac{9z^4}{8}\)
=> \(M=\left(x^4+y^4+z^4\right)\left(\frac{1}{x^4}+\frac{1}{y^4}+\frac{1}{z^4}\right)\ge\frac{33}{z^4}.\frac{9z^4}{8}=\frac{297}{8}\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(\hept{\begin{cases}x=y\\x+y=-z\\x^2+y^2=\frac{z^2}{2}\end{cases}}\Leftrightarrow x=y=\frac{-z}{2}\)
...
HD
1
17 tháng 12 2016
Điểm cực tiểu A(0;-2), điểm cực đại B(2;2)
Mình không hiểu đề bài yêu cầu tìm đường thẳng đi qua điểm A và B, đi qua cả A và B hay là các tiếp tuyến tại A và B?
MO
14 tháng 12 2016
nếu có đáp án trắc nghiệm thì theo mình làm bài này nhanh như sau:
tìm tập xác định D=R
tính y', tìm điều kiện để cho hàm số có 3 điểm cực trị là pt y'=0 có 3 nghiệm phân biệt
áp dụng công thức tính nhanh :b^2 -6ac, suy ra m , kết hợp với điều kiện hàm số có 3 điểm cực trị, suy ra m cần tìm
lưu ý: công thức mình đưa ra là b^2-6ac chỉ áp dụng cho hàm bậc 4 trùng phương, 3 điểm cực trị là 3 đỉnh của tam giác và có trọng tâm là gốc tọa độ.
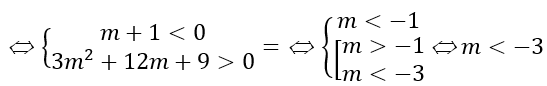
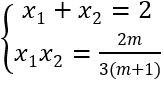
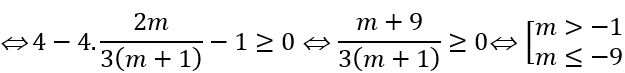
=??????????????? nha