K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
27 tháng 1 2017
Chọn C.
Điều kiện. x ≠ -1
Phương trình tương đương 
Lấy ln hai vế của , ta được 
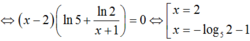
Suy ra x0 = 2 và P = 60.
CM
9 tháng 3 2019
Đáp án là A
Theo điều đủ để hàm số có cực trị thì x 0 là điểm cực tiểu của hàm số.
CM
30 tháng 11 2017
Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 3 2019
\(I=\int\limits^{100}_0x\left(x-1\right)...\left(x-100\right)dx\)
Đặt \(100-x=t\Rightarrow dx=-dt;\left\{{}\begin{matrix}x=0\Rightarrow t=100\\x=100\Rightarrow t=0\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^0_{100}\left(100-t\right)\left(99-t\right)...\left(1-t\right)\left(-t\right).\left(-dt\right)\)
\(I=\int\limits^0_{100}\left(-1\right)\left(t-100\right).\left(-1\right)\left(t-99\right)...\left(-1\right)\left(t-1\right)\left(-1\right)t\left(-dt\right)\) (101 số -1)
\(I=-\int\limits^0_{100}t\left(t-1\right)\left(t-2\right)...\left(t-100\right)\left(-dt\right)\)
\(I=-\int\limits^{100}_0t\left(t-1\right)\left(t-2\right)...\left(t-100\right)dt\)
\(I=-\int\limits^{100}_0x\left(x-1\right)\left(x-2\right)...\left(x-100\right)dx=-I\)
\(\Rightarrow2I=0\Rightarrow I=0\)
CM
4 tháng 12 2019
Chọn D.
Gọi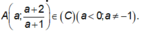 
Phương trình tiếp tuyến của (C) tại A là:
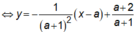
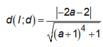
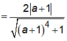
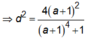
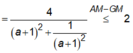
Dấu “=” xảy ra khi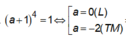 
=> M(-2;0)
Suy ra 
CM
21 tháng 1 2018
Đáp án D
Điểu kiện
Xét -6 < x < 4, khi đó áp dụng công thức 
ta có:
=> hàm số đã cho nghịch biến trên -6 < x ≤ 4
Vì vậy, hàm số đạt giá trị nhỏ nhất tại x0 = 4
đáp án 0
1001001000 * 0 = 0