Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(C=\dfrac{1}{2}+\dfrac{1}{14}+\dfrac{1}{35}+\dfrac{1}{65}+\dfrac{1}{104}+\dfrac{1}{152}\)
\(=\dfrac{2}{4}+\dfrac{2}{28}+\dfrac{2}{70}+\dfrac{2}{130}+\dfrac{2}{208}+\dfrac{2}{304}\)
\(=\dfrac{2}{1.4}+\dfrac{2}{4.7}+\dfrac{2}{7.10}+\dfrac{2}{10.13}+\dfrac{2}{13.16}+\dfrac{2}{16.19}\)
\(=\dfrac{2}{3}.\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{13}-\dfrac{1}{16}+\dfrac{1}{16}-\dfrac{1}{19}\right)\)
\(=\dfrac{2}{3}.\left(1-\dfrac{1}{19}\right)\)
\(=\dfrac{2}{3}.\dfrac{18}{19}=\dfrac{12}{19}\)

Ta có :
\(C=\dfrac{1}{2}+\dfrac{1}{14}+\dfrac{1}{35}+\dfrac{1}{65}+\dfrac{1}{104}+\dfrac{1}{152}\)
\(C=\dfrac{1}{1.2}+\dfrac{1}{2.7}+\dfrac{1}{7.5}+\dfrac{1}{5.13}+\dfrac{1}{13.16}+\dfrac{1}{16.19}\)
\(C=\dfrac{2}{3}\left(\dfrac{3}{1.4}+\dfrac{3}{4.7}+\dfrac{3}{7.10}+\dfrac{3}{10.13}+\dfrac{3}{13.16}+\dfrac{3}{16.19}\right)\)
\(C=\dfrac{2}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{16}+\dfrac{1}{16}-\dfrac{1}{19}\right)\)
\(C=\dfrac{2}{3}\left(1-\dfrac{1}{19}\right)\)
\(C=\dfrac{2}{3}.\dfrac{18}{19}=\dfrac{12}{19}\)
~ Học tốt ~

\(C=\dfrac{1}{2}+\dfrac{1}{14}+\dfrac{1}{35}+\dfrac{1}{65}+\dfrac{1}{104}+\dfrac{1}{152}\)
\(=\dfrac{2}{4}+\dfrac{2}{28}+\dfrac{2}{70}+\dfrac{2}{130}+\dfrac{2}{208}+\dfrac{2}{304}\)
\(=\dfrac{2}{1\cdot4}+\dfrac{2}{4\cdot7}+\dfrac{2}{7\cdot10}+\dfrac{2}{10\cdot13}+\dfrac{2}{13\cdot16}+\dfrac{2}{16\cdot19}\)
\(=\dfrac{2}{3}\left(\dfrac{3}{1\cdot4}+\dfrac{3}{4\cdot7}+\dfrac{3}{7\cdot10}+...+\dfrac{3}{16\cdot19}\right)\)
\(=\dfrac{2}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{16}-\dfrac{1}{19}\right)\)
\(=\dfrac{2}{3}\left(1-\dfrac{1}{19}\right)=\dfrac{2}{3}\cdot\dfrac{18}{19}=\dfrac{12}{19}\)
Ta có :
\(C=\dfrac{1}{2}+\dfrac{1}{14}+\dfrac{1}{35}+\dfrac{1}{65}+\dfrac{1}{104}+\dfrac{1}{152}\)
\(\Rightarrow C=\dfrac{2}{4}+\dfrac{2}{28}+\dfrac{2}{70}+\dfrac{2}{130}+\dfrac{2}{208}+\dfrac{2}{304}\)
\(=\dfrac{2}{3}\left(\dfrac{3}{1\cdot4\cdot+4}+\dfrac{3}{4\cdot7}+\dfrac{3}{7\cdot10}+\dfrac{3}{10\cdot13}+\dfrac{3}{13\cdot16}+\dfrac{3}{16\cdot19}\right)\)
\(=\dfrac{2}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{16}-\dfrac{1}{19}\right)\)
\(=\dfrac{2}{3}\left(1-\dfrac{1}{19}\right)\)
\(=\dfrac{2}{3}\cdot\dfrac{18}{19}\)
\(=\dfrac{12}{19}\)

I. Tính:
1) \(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}\)
\(=\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}\)
\(=1-\dfrac{1}{6}\)
\(=\dfrac{5}{6}\)
2) \(\dfrac{2}{15}+\dfrac{2}{35}+\dfrac{2}{63}+\dfrac{2}{99}+\dfrac{2}{143}\)
\(=\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+\dfrac{2}{9.11}+\dfrac{2}{11.13}\)
\(=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{13}\)
\(=\dfrac{1}{3}-\dfrac{1}{13}\)
\(=\dfrac{13}{39}-\dfrac{3}{39}=\dfrac{10}{39}\)
II. Tìm x:
\(1\dfrac{3}{5}+\left(\dfrac{\dfrac{2}{171}}{\dfrac{5}{171}}+\dfrac{\dfrac{2}{373}}{\dfrac{5}{373}}\right)x=\dfrac{16}{5}\)
\(\dfrac{8}{5}+\left[\dfrac{2\left(\dfrac{1}{171}+\dfrac{1}{373}\right)}{5\left(\dfrac{1}{171}+\dfrac{1}{373}\right)}\right]x=\dfrac{16}{5}\)
\(\dfrac{8}{5}+\dfrac{2}{5}x=\dfrac{16}{5}\)
\(\dfrac{2}{5}x=\dfrac{16}{5}-\dfrac{8}{5}\)
\(\dfrac{2}{5}x=\dfrac{8}{5}\)
\(x=\dfrac{8}{5}:\dfrac{2}{5}\)
\(x=4\)

1/
a) ta có \(\dfrac{1}{1.4}+\dfrac{1}{4.7}+...+\dfrac{1}{97.100}=\dfrac{1}{3}.\left(\dfrac{3}{1.4}+\dfrac{3}{4.7}+...+\dfrac{3}{97.100}\right)\)
\(=\dfrac{1}{3}.\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{97}-\dfrac{1}{100}\right)\)
\(=\dfrac{1}{3}.\dfrac{99}{100}=\dfrac{33}{100}\)
⇒ \(\dfrac{33}{100}=\dfrac{0,33x}{2009}\)
⇒ \(\dfrac{33}{100}=\dfrac{0,33}{2009}.x\Rightarrow x=\dfrac{33}{100}:\dfrac{0,33}{2009}=2009\)
b,1 + 1/3 + 1/6 + 1/10 + ... + 2/x(x+1)=1 1991/1993
2 + 2/6 + 2/12 + 2/20 + ... + 2/x(x+1) = 3984/1993
2.(1/1.2 + 1/2.3 + 1/3.4 + ... + 1/x(x+1) = 3984/1993
2.(1 − 1/2 + 1/2 − 1/3 + ... + 1/x − 1/x+1)=3984/1993
2.(1 − 1/x+1) = 3984/1993
1 − 1/x + 1= 3984/1993 :2
1 − 1/x+1 = 1992/1993
1/x+1 = 1 − 1992/1993
1/x+1=1/1993
<=>x+1 = 1993
<=>x+1=1993
<=> x+1=1993
<=> x = 1993-1
<=> x = 1992

\(C=\dfrac{2}{15}+\dfrac{2}{35}+\dfrac{2}{63}+...+\dfrac{2}{399}\)
\(C=\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+...+\dfrac{2}{19.21}\)
\(C=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{19}-\dfrac{1}{21}\)
\(C=\dfrac{1}{3}-\dfrac{1}{21}\)
\(C=\dfrac{2}{7}\)

\(D=\dfrac{1}{2}+\dfrac{-1}{5}+\dfrac{-5}{7}+\dfrac{1}{6}+\dfrac{-3}{35}+\dfrac{1}{3}+\dfrac{1}{41}\)
\(D=\left(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{3}\right)+\left(\dfrac{-1}{5}+\dfrac{-5}{7}+\dfrac{-3}{35}\right)+\dfrac{1}{41}\)
\(D=1+-1+\dfrac{1}{41}\)
\(D=0+\dfrac{1}{41}\)
\(D=\dfrac{1}{41}\)
\(C=\left(\dfrac{1}{3}+\dfrac{3}{5}+\dfrac{1}{15}\right)+\left(\dfrac{-3}{4}+\dfrac{-1}{36}+\dfrac{-2}{9}\right)+\dfrac{1}{57}\)
\(=\dfrac{5+9+1}{15}+\dfrac{-27-1-8}{36}+\dfrac{1}{57}\)
=1/57
\(E=\left(-\dfrac{1}{2}-\dfrac{1}{9}-\dfrac{7}{18}\right)+\left(\dfrac{3}{5}+\dfrac{4}{35}+\dfrac{2}{7}\right)+\dfrac{1}{127}=\dfrac{1}{127}\)

=1/1.2+1/2.7+1/7.5+1/5.13+1/13.8+1/8.19=2/1.4+2/4.7+2/7.10+2/10.13+2/13.16+2/16.19(ca tu va mau cung nhan them 2 gia tri khong doi)=2/3.(3/1.4+3/4.7+3/7.10+3/10.13+3/13.16+3/16.19)=2/3.(1/1-1/4+1/4-1/7+1/7-1/10+1/101/13+1/13-1/16+1/16-1/19)=2/3.18/19=12/19

\(A=\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{9900}\)
\(A=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{99\cdot100}\)
\(A=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(A=1-\dfrac{1}{100}=\dfrac{99}{100}\)
\(B=\dfrac{1}{3}+\dfrac{1}{15}+\dfrac{1}{35}+..+\dfrac{1}{195}\) ( là 195 ms đúng ! )
\(B=\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+...+\dfrac{1}{13\cdot15}\)
\(B=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{13}-\dfrac{1}{15}\right)\)
\(B=\dfrac{1}{2}\left(1-\dfrac{1}{15}\right)=\dfrac{1}{2}\cdot\dfrac{14}{15}=\dfrac{7}{15}\)
\(C=\dfrac{1}{2\cdot4}+\dfrac{1}{4\cdot6}+\dfrac{1}{6\cdot8}+...+\dfrac{1}{98\cdot100}\)
Rồi làm tương tự cân b nha!
\(D=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{19}+\dfrac{1}{19}-\dfrac{1}{32}+\dfrac{1}{32}-\dfrac{1}{57}\)
\(+\dfrac{1}{57}-\dfrac{1}{87}\)
\(D=\dfrac{1}{3}-\dfrac{1}{87}=\dfrac{28}{87}\)
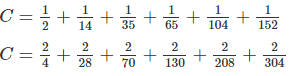
1. Tính nhanh:
\(\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}\)
\(=\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}\)
\(=\dfrac{1}{2}-\dfrac{1}{8}\)
\(=\dfrac{3}{8}\)
2. Tính nhanh
Đặt \(A\) = \(\dfrac{1}{15}+\dfrac{1}{35}+\dfrac{1}{63}+\dfrac{1}{99}+\dfrac{1}{143}\)
\(A\) \(=\dfrac{1}{3.5}+\dfrac{1}{5.7}+\dfrac{1}{7.9}+\dfrac{1}{9.11}+\dfrac{1}{11.13}\)
\(2A=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{13}\)
\(2A=\dfrac{1}{3}-\dfrac{1}{13}\)
\(2A=\dfrac{10}{39}\)
\(A=\dfrac{10}{39}:2\)
\(A=\dfrac{5}{39}\)