Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D O M N E F
a) Giả sử \(\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{OC}-\overrightarrow{OB}-\overrightarrow{OD}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{BO}+\overrightarrow{OC}+\overrightarrow{DO}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{BO}+\overrightarrow{OA}\right)+\left(\overrightarrow{DO}+\overrightarrow{OC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{0}\) (đúng do tứ giác ABCD là hình bình hành).
b) \(\overrightarrow{ME}+\overrightarrow{FN}=\overrightarrow{MA}+\overrightarrow{AE}+\overrightarrow{FC}+\overrightarrow{CN}\)
\(=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\).
Do các tứ giác AMOE, MOFB, OFCN, EOND cũng là các hình bình hành.
Vì vậy \(\overrightarrow{CN}=\overrightarrow{FO}=\overrightarrow{BM};\overrightarrow{FC}=\overrightarrow{ON}=\overrightarrow{ED}\).
Do đó: \(\overrightarrow{ME}+\overrightarrow{FN}=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\)
\(=\left(\overrightarrow{MA}+\overrightarrow{BM}\right)+\left(\overrightarrow{AE}+\overrightarrow{ED}\right)\)
\(=\overrightarrow{BA}+\overrightarrow{AD}=\overrightarrow{BD}\) (Đpcm).

a: Xét tứ giác ABDE có
AB//DE
AB=DE
=>ABDE là hình bình hành
b: Xét ΔIAB và ΔICD có
góc IAB=góc ICD
góc AIB=góc CID
=>ΔIAB đồng dạng với ΔICD
=>IA/IC=IB/ID=AB/CD=3/14
=>IA/3=IC/14=(IA+IC)/(3+14)=15/17
=>IA=45/17cm; IC=210/17cm
c: IB/ID=3/14
=>IB/3=ID/14=(IB+ID)/(3+14)=8/17
=>ID=112/17(cm)
IC=210/17; ID=112/17; CD=14
IC^2+ID^2=(210/17)^2+(112/17)^2=196
CD^2=14^2=196
=>IC^2+ID^2=CD^2
=>ΔICD vuông tại I
d: S ABCD=1/2*AC*BD=1/2*8*15=4*15=60

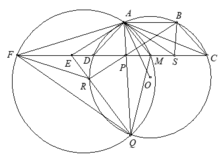
2). Vì EA là tiếp xúc (O) và từ kết quả câu 1) ta có E A 2 = E R . E Q = E P 2 .
Từ đó có E A = E P ⇒ D A P ^ = E A P ^ − E A D ^ = A P E ^ − A C D ^ = P A C ^
Do đó AP là phân giác D A C ^ ⇒ Q C = Q D ⇒ Q M ⊥ C D
51 nhá