Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E I H 1 2 1 2 1 1 2 1
a) Từ I kẻ IH vuông góc với BC
Xét t/giác BID và BIH
có: \(\widehat{B_1}=\widehat{B_2}\)(gt)
BI: chung
\(\widehat{BDI}=\widehat{BHI}=90^0\)
=> t/giác BID = t/giác BID (ch.gn)
=> DI = IH (2 cạnh t/ứng) (1)
CMTT: t/giác ECI = t/giác HCI (ch - gn)
=> EI = IH (2)
Từ (1) và (2) => DI = IE
Nối A và I
TA có: AH // IE (vì cùng vuông góc với AC) => \(\widehat{DAI}=\widehat{AIE}\)(slt)
Xét t/giác DAI và t/giác EIA
có: IA : chung
\(\widehat{ADI}=\widehat{IEA}=90^0\)(gt)
\(\widehat{DAI}=\widehat{AIE}\)(cmt)
=> t/goác DAI = t/giác EIA (ch - gn)
=> DI = EA; AD = EI (các cặp cạnh tương ứng)
mà DI = EI (cmt)
=> AE = AD (đpcm)
b) Xét t/giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2 (định lí Pi - ta - go)
=> BC2 = 62 + 82 = 100
=> BC = 10 (cm)
Ta có: t/giác BID = t/giác BIH (cmt) => BD = BH (2 cạnh t/ứng)
t/giác CIE = t/giác CIH (cmt) => CH = EC (2 cạnh t/ứng)
=> BD + EC = DH + HC = BC = 10 cm
Ta lại có: AB + AC = BD + AD + AE + EC = (BD + EC) + 2AD = 6 + 8
=> 2AD + 10 = 14
=> 2AD = 4 => AD = AE = 2 cm
A B C I D E K
a) Vì I là giao điểm của phân giác \(\widehat{B}\)và \(\widehat{C}\)
=> AI là phân giác \(\widehat{A}\)
=> ID=IE (1)
\(\Delta ADI\)và \(\Delta AEI\)vuông cân
=> ID=AD; IE=AE (2)
Từ (1)(2) => ED=AE (đpcm)
b) Hạ IK _|_ BC; ID _|_ AB; IE _|_ AC
=> BD=BK; CK=CE; AD=AE
\(\Delta ABC\)vuông tại A có AB=6cm; AC=8cm. Áp dụng định lý Pytago ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow BC=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10\left(cm\right)\)
Đặt AD=x => BK=6-x; CK=8-c
=> 6-x+8-x=10
=> x=2
Vậy AD=2cm

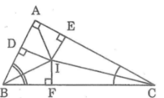
A B C D E F I
a) AI là tai phân giác của góc A nên ID = IE. (1)
Các tam giác vuông ADI, AEI có \(\widehat{DAI}=\widehat{EAI}=45^o\) nên là tam giác vuông cân, do đó AD = ID, AE = IE. (2)
Từ (1) và (2) suy ra AD = AE.
b) Áp dụng định lí Py-ta-go trong tam giác vuông ABC:
BC2 = AB2 + AC2 = 62 + 82
BC2 = 36 + 64 = 100
\(\Rightarrow BC=\sqrt{100}=10\left(cm\right)\).
Kẻ IF \(\perp\) BC
Xét hai tam giác vuông IBD và IBF có:
BI: cạnh huyền chung
\(\widehat{IBD}=\widehat{IBF}\) (gt)
Vậy: \(\Delta IBD=\Delta IBF\left(ch-gn\right)\)
\(\Rightarrow\) BD = BF (hai cạnh tương ứng)
Xét hai tam giác vuông ICE và ICF có:
CI: cạnh huyền chung
\(\widehat{ICE}=\widehat{ICF}\left(gt\right)\)
Vậy: \(\Delta ICE=\Delta ICF\left(ch-gn\right)\)
Suy ra: CE = CF (hai cạnh tương ứng)
Ta có: AB + AC - BC = AD + DB + AE + EC - BF - CF.
Do BD = BF, CE = CF nên:
AB + AC - BC = AD + AE
\(\Rightarrow\) 6 + 8 - 10 = AD + AE
\(\Rightarrow\) AD + AE = 4 (cm).
Theo câu a) ta có AD = AE nên AD = AE = 2cm.
Hình tự vẽ nhé!!!![]()
a) AI là tai phân giác của góc A nên ID = IE. (1)
Các tam giác vuông ADI, AEI có ˆDAI=ˆEAI=45oDAI^=EAI^=45o nên là tam giác vuông cân, do đó AD = ID, AE = IE. (2)
Từ (1) và (2) suy ra AD = AE.
b) Áp dụng định lí Py-ta-go trong tam giác vuông ABC:
BC2 = AB2 + AC2 = 62 + 82
BC2 = 36 + 64 = 100
⇒BC=√100=10(cm)⇒BC=100=10(cm).
Kẻ IF ⊥⊥ BC
Xét hai tam giác vuông IBD và IBF có:
BI: cạnh huyền chung
ˆIBD=ˆIBFIBD^=IBF^ (gt)
Vậy: ΔIBD=ΔIBF(ch−gn)ΔIBD=ΔIBF(ch−gn)
⇒⇒ BD = BF (hai cạnh tương ứng)
Xét hai tam giác vuông ICE và ICF có:
CI: cạnh huyền chung
ˆICE=ˆICF(gt)ICE^=ICF^(gt)
Vậy: ΔICE=ΔICF(ch−gn)ΔICE=ΔICF(ch−gn)
Suy ra: CE = CF (hai cạnh tương ứng)
Ta có: AB + AC - BC = AD + DB + AE + EC - BF - CF.
Do BD = BF, CE = CF nên:
AB + AC - BC = AD + AE
⇒⇒ 6 + 8 - 10 = AD + AE
⇒⇒ AD + AE = 4 (cm).
Theo câu a) ta có AD = AE nên AD = AE = 2cm.

Tam giác vuông BAC có ∠A = 90o
Áp dụng định lí Pitago, ta có:
BC2 = AB2 + AC2
= 62 + 82 = 36 + 64 = 100
⇒ BC = 10 (cm)
Kẻ IF ⊥ BC
Xét hai tam giác vuông IDB và IFB, ta có:
∠(IDB) = ∠(IFB) = 90o
∠(DBI) = ∠(FBI) (gt)
cạnh huyền BI chung
Suy ra: ΔIDB = ΔIFB (cạnh huyền, góc nhọn)
Suy ra: DB = FB (hai cạnh tương ứng) (4)
Xét hai tam giác vuông IEC và IFC, ta có:
∠(IEC) = ∠(IFC) = 90o
∠(ECI) = ∠(FCI) (gt)
cạnh huyền CI chung
Suy ra: ΔIEC = ΔIFC (cạnh huyền, góc nhọn)
Suy ra: CE = CF (hai cạnh tương ứng) (5)
Mà: AD + AE = AB - DB + AC - CE
Suy ra: AD + AE = AB + AC - (DB + CE) (6)
Từ (4), (5) và (6) suy ra: AD + AE = AB + AC - (FB + FC)
= AB + AC - BC = 6 + 8 - 10 = 4 (cm)
Mà AD = AE (chứng minh trên)
Nên AD = AE = 4 : 2 = 2(cm).