Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Độ cao của máy bay là CD, độ dài AB = 60m; D A C ^ = 30 0 ; D B C ^ = 50 0
Gọi BC = x => AC = 60 + x
Xét tam giác BDC vuông tại C có:
![]()
Xét tam giác ADC vuông tại C có:
![]()
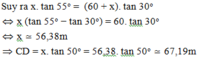
Vậy độ cao của máy bay so với mặt đất là 67,19m
Đáp án cần chọn là: C

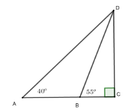
Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m
Đáp án cần chọn là: A

Để tính vận tốc trung bình của máy bay, ta cần biết quãng đường máy bay đã bay và thời gian máy bay bay. Quãng đường máy bay đã bay có thể tính bằng cách sử dụng định lý Pythagoras trong tam giác vuông. Ta có: quãng đường = độ cao / sin(góc nâng) = 10 km / sin(30°) = 20 km Thời gian máy bay bay là 2,4 phút = 2,4/60 = 0,04 giờ. Vận tốc trung bình của máy bay được tính bằng cách chia quãng đường máy bay đã bay cho thời gian máy bay bay: vận tốc trung bình = quãng đường / thời gian = 20 km / 0,04 giờ = 500 km/h Vậy, vận tốc trung bình của máy bay là 500 km/h.

Gọi C là vị trí của máy bay
Gọi CH là độ cao của máy bay so với mặt đất
=>CH\(\perp\)AB tại H
Ta có hình vẽ sau:
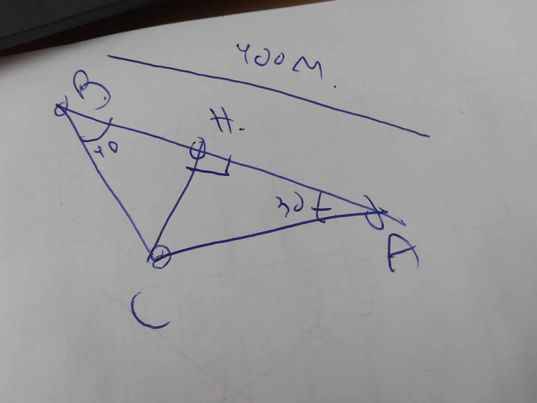
Xét ΔCBA có \(\widehat{CBA}+\widehat{CAB}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+30^0+40^0=180^0\)
=>\(\widehat{ACB}=110^0\)
Xét ΔABC có \(\dfrac{BA}{sinACB}=\dfrac{AC}{sinB}=\dfrac{BC}{sinA}\)
=>\(\dfrac{400}{sin110}=\dfrac{AC}{sin40}=\dfrac{BC}{sin30}\)
=>\(AC\simeq273,62\left(m\right);BC\simeq212,84\left(m\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinACB\)
\(=\dfrac{1}{2}\cdot273,62\cdot212,84\cdot sin110\simeq27362,57\left(m^2\right)\)
Xét ΔACB có CH là đường cao
nên \(\dfrac{1}{2}\cdot CH\cdot AB=S_{ABC}\)
=>\(CH\cdot\dfrac{400}{2}=27362,57\)
=>\(CH\simeq136,81\left(m\right)\)

Gọi giao điểm của đường nhìn thấy máy bay tại A và B là C.
Vẽ CH vuông góc AB
=>CH là độ cao của máy bay
góc ACB=180-40-32=108 độ
Xét ΔACB có
AB/sin C=AC/sinB=BC/sin A
=>400/sin108=AC/sin32=BC/sin40
=>\(AC\simeq222,9\left(m\right);BC\simeq270,3\left(m\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinC=\dfrac{1}{2}\cdot222.9\cdot270.3\cdot sin108\simeq28650,52\left(m^2\right)\)
Độ cao là:"
28650,52*2/400\(\simeq143\left(m\right)\)

Gọi hai điểm trên mặt đất là A,B
Đỉnh của ngọn núi là C
Theo đề, ta có: góc A=40 độ; góc B=32 độ; AB=1km
góc C=180-40-32=108 độ
Xét ΔABC có AB/sinC=AC/sinB=BC/sinA
=>AC\(\simeq\)0,56(km); CB\(\simeq\)0,68(km)
S CAB=1/2*0,56*0,68*sin108
\(\simeq0,18\left(km^2\right)\)
Chiều cao của ngọn núi là;
0,18*2:1=0,36(km)