DT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
15 tháng 5 2017
Gọi giá tiền mỗi quả cam là x, giá tiền mỗi quả bưởi là y ta có hệ hai phương trình
10x+7y=17800 (1)
12x+6y=18000 (2)
Giải hệ trên để tìm x và y
14 tháng 5 2016
Gọi x (đồng) là giá tiền một quả quýt và y (đồng) là giá tiền một quả cam. Điều kiện
x > 0, y > 0 ta có hệ phương trình:
<=> <=>
<=> .
Trả lời: Giá tiền một quả quýt: 800 đồng, một quả cam 1400 đồng
Chúc bạn học tốt!
NH
14
TD
9 tháng 1 2017
Gọi số quả quýt là x (0<x<17)
Gọi số quả cam là y (0<x<17)
tổng số quả cam và quýt là 17 nên ta có pt:x+y=17 (1)
vì một quả cảm chia thành 7 miếng nên y quả cảm chia thành 10y
vì một quả quýt chia thành 3 miếng nên x qua quýt chia thành 3x
vì tổng các miếng cam và quýt là 100 miếng nên ta có pt :3x+7y=100 (2)
từ (1) và (2) ta có hpt \(\left\{\begin{matrix}x+y=17\\3x+10y=100\end{matrix}\right.\Leftrightarrow\left\{\begin{matrix}x=10\\y=7\end{matrix}\right.\)
vậy số quả cam là 7 số qủa quýt là 10
VK
4 tháng 4 2017
Gọi số cam là x ( quả )
số quýt là y (quả)
Điều kiện x, y > 0
Theo đề bài ta có hệ phương trình :
\(\left\{{}\begin{matrix}x+y=7\left(1\right)\\10x+3y=100\left(2\right)\end{matrix}\right.\)
(1) ⇔ y = 17 - x (3)
Thế (3) vào (2): 10x + 3(17 - x) = 100
⇔ 10x + 51 - 3x = 100 ⇔ 7x = 49 ⇔ x = 7
Từ đó y = 17 - 7 = 10
Vậy có 7 quả cam và 10 quả quýt.
S
5 tháng 5 2020
Xét 2 tập hợp \(A=\left\{1;2;3;....;25000\right\}\) và \(B=\left\{1;3;3\cdot2;3\cdot2^2;.....;3\cdot2^{13}\right\}\)
Mà \(3\cdot2^{13}=24576< 25000\)
\(\Rightarrow B\subset A\)
Do tập B có 15 phần tử, mỗi quả bóng được sơn 1 màu mà có 7 màu nên theo nguyên lý Dirichlet tồn tại 3 quả bóng cùng màu
Giả sử 3 quả bóng đó được đánh số a > b > c thì \(a⋮b;b⋮c\) và \(abc\ge18>17\)
Vậy ta có đpcm
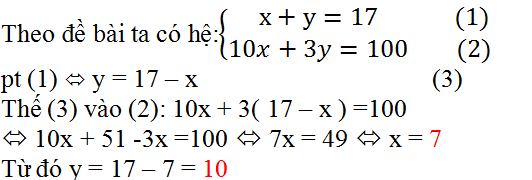
Giống nửa uqar cam còn lại
Nửa quả cam giống nửa quả cam còn lại(vì cùng 1 quả cam)